A Regra de Sturges
A Regra de Sturges permite estimar o número ideal de classes para montar uma distribuição de frequência. É um recurso clássico da estatística descritiva, equilibrando detalhe e legibilidade em planilhas, relatórios e gráficos estatísticos.

Fórmula
Onde \(k\) é o número de classes e \(n\) o total de observações (logaritmo decimal).
Exemplo rápido
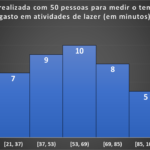
Dados: \(n = 200\).
Aplicando a fórmula: \(k \approx 1 + 3{,}322 \cdot \log_{10}(200) \approx 1 + 3{,}322 \cdot 2{,}3010 \approx \mathbf{9}\).
Resultado: usar cerca de 9 classes.
Exercícios Resolvidos
Exercício 1 — Número de classes (básico)
Uma amostra possui n = 500. Determine \(k\).
👀 Ver solução
\( \log_{10}(500) \approx 2{,}6990 \Rightarrow k \approx 1 + 3{,}322 \cdot 2{,}6990 \approx \mathbf{10} \) classes.
Exercício 2 — Construção da tabela (passo a passo)
Contexto: Notas de uma prova variam de 0 a 100 (inteiros), com n = 1.000 registros.
👀 Ver passo a passo
Passo 1 — Número de classes: \(k = 1 + 3{,}322 \cdot \log_{10}(1000) = 1 + 3{,}322 \cdot 3 = 10{,}966 \Rightarrow \boxed{11}\).
Passo 2 — Amplitude total (R): \(R = 100 – 0 = \boxed{100}\).
Passo 3 — Largura (h): \(h = R/k \approx 100/11 \approx 9{,}09 \Rightarrow\) adote \(\boxed{h = 10}\) para cobrir todo o alcance.
Passo 4 — Classes (semiabertas \([L_i, L_s)\)): [0,10), [10,20), …, [90,100), [100,110).
Passo 5 — Tabela ilustrativa (frequências exemplificativas que somam 1000):
| Classe | Intervalo | Limites Reais | Ponto Médio (xi) | f | F (acum.) | fr | fr (%) |
|---|---|---|---|---|---|---|---|
| 1 | [0,10) | −0,5 a 9,5 | 5 | 40 | 40 | 0,040 | 4,0% |
| 2 | [10,20) | 9,5 a 19,5 | 15 | 75 | 115 | 0,075 | 7,5% |
| 3 | [20,30) | 19,5 a 29,5 | 25 | 120 | 235 | 0,120 | 12,0% |
| 4 | [30,40) | 29,5 a 39,5 | 35 | 150 | 385 | 0,150 | 15,0% |
| 5 | [40,50) | 39,5 a 49,5 | 45 | 190 | 575 | 0,190 | 19,0% |
| 6 | [50,60) | 49,5 a 59,5 | 55 | 160 | 735 | 0,160 | 16,0% |
| 7 | [60,70) | 59,5 a 69,5 | 65 | 120 | 855 | 0,120 | 12,0% |
| 8 | [70,80) | 69,5 a 79,5 | 75 | 80 | 935 | 0,080 | 8,0% |
| 9 | [80,90) | 79,5 a 89,5 | 85 | 45 | 980 | 0,045 | 4,5% |
| 10 | [90,100) | 89,5 a 99,5 | 95 | 15 | 995 | 0,015 | 1,5% |
| 11 | [100,110) | 99,5 a 109,5 | 105 | 5 | 1000 | 0,005 | 0,5% |
| Totais | 1000 | — | 1,000 | 100% | |||
Passo 6 — Leitura: maior concentração entre 40 e 60 pontos; percentuais acumulados ajudam a localizar mediana e quartis.
Mais exercícios sobre a Regra de Sturges
Exercício 3 — Número de classes (básico)
Uma amostra possui n = 120. Determine o número ideal de classes.
👀 Ver solução
\( \log_{10}(120) \approx 2{,}07918 \Rightarrow k \approx 1 + 3{,}322 \cdot 2{,}07918 = 7{,}907 \Rightarrow \boxed{8} \) classes.
Exercício 4 — k, largura e intervalos (intermediário)
Dados: n = 850, mínimo 12, máximo 97. Calcule \(k\), \(h\) e proponha intervalos.
👀 Ver solução
- \( k = 1 + 3{,}322 \cdot \log_{10}(850) \approx 10{,}732 \Rightarrow \boxed{11} \).
- \( R = 97 – 12 = \boxed{85} \).
- \( h = R/k \approx 85/11 \approx \boxed{7{,}73} \) (pode arredondar para \(h = 8\)).
- Intervalos sugeridos: [12,20), [20,28), …, [92,100).
Exercício 5 — Identificação de classe (avançado)
Para \(n = 1000\) e notas de 0 a 100, com \(k \approx 11\) e \(h = 10\), em qual classe está a nota 73?
👀 Ver solução
\( i = \left\lfloor \dfrac{73 – 0}{10} \right\rfloor + 1 = 8 \Rightarrow \) classe \([70,80)\).
📘 Turbine seus estudos de Estatística
Materiais visuais e práticos para aprender mais rápido:
🚀 Mapas Mentais 📚 10 eBooks 📝 Banco de Questões 🎯 ENEM Matemática 📢 Canais Oficiais