A regra de três composta é uma ferramenta da matemática básica essencial para resolver problemas matemáticos que envolvem várias grandezas proporcionais. Este artigo tem como objetivo explicar de forma simples e prática como utilizar essa técnica, abordando desde os conceitos básicos até a resolução de exercícios.
O Que é a Regra de Três Composta?
A regra de três composta é um método que nos permite encontrar um valor desconhecido quando estamos lidando com três ou mais grandezas proporcionais. Essas grandezas podem ser direta ou inversamente proporcionais. A diferença fundamental entre a regra de três simples e a composta é o número de grandezas envolvidas. Enquanto na regra de três simples lidamos com apenas duas grandezas, na composta trabalhamos com três ou mais.
Passos Para Resolver a Regra de Três Composta
Para resolver problemas que envolvem a regra de três composta, siga os passos abaixo:
- Identificação das Grandezas: Determine quais são as grandezas envolvidas no problema.
- Construção da Tabela: Organize as grandezas em uma tabela, colocando a grandeza que contém a incógnita em destaque.
- Análise da Proporção: Verifique a relação entre as grandezas, identificando se são direta ou inversamente proporcionais.
- Montagem e Resolução da Equação: Monte a equação baseada na relação entre as grandezas e resolva para encontrar o valor desconhecido.
Exemplo 1: Regra de Três Composta com Três Grandezas
Problema: Uma construtora foi contratada para reformar todas as escolas de uma cidade. Sabemos que 4 pintores levariam 8 dias para pintar 6 escolas. Quanto tempo 8 pintores levariam para pintar 18 escolas?
Resolução:
- Grandezas: Pintores, dias (incógnita), escolas.
- Construção da Tabela:
| Pintores | Dias (X) | Escolas |
|---|---|---|
| 4 | 8 | 6 |
| 8 | X | 18 |
- Análise das Relações:
- Dias e Pintores: Mais pintores reduzem o tempo (relação inversa).
- Dias e Escolas: Mais escolas aumentam o tempo (relação direta).
- Montagem da Equação:
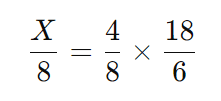
Agora, simplificando as frações:
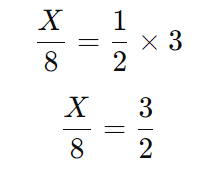
Multiplicando ambos os lados por 8:
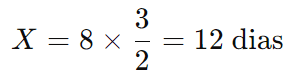
Resposta: 8 pintores levariam 12 dias para pintar 18 escolas.
Lista de Exercício Regra de Três
Exemplo 2: Regra de Três Composta com Quatro Grandezas
Problema: Em uma fábrica, 3 máquinas trabalhando 5 dias por 4 horas produzem 4.000 peças. Se uma máquina quebrar e o tempo de trabalho aumentar para 6 dias e 8 horas diárias, quantas peças serão produzidas?
Resolução:
- Grandezas: Máquinas, dias, horas, peças (incógnita).
- Construção da Tabela:
| Máquinas | Dias | Horas | Peças (Y) |
|---|---|---|---|
| 3 | 5 | 4 | 4000 |
| 2 | 6 | 8 | Y |
- Análise das Relações:
- Mais máquinas produzem mais peças (direta).
- Mais dias e horas aumentam a produção (direta).
- Montagem da Equação:
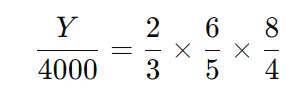
Resolva a equação:
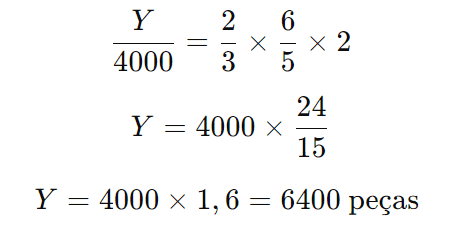
Resposta: Serão produzidas 6.400 peças.
Diferença Entre Regra de Três Simples e Composta
A regra de três simples é utilizada quando lidamos com apenas duas grandezas. Por exemplo, se sabemos que 2 pintores pintam 4 paredes em 3 dias, podemos calcular quantas paredes 4 pintores pintariam no mesmo período. Já a regra de três composta é usada em cenários mais complexos, onde estão envolvidas mais de duas grandezas, como vimos nos exemplos anteriores.
Exercício Resolvido
Questão: Uma indústria tem um reservatório de 900 m³ que escoa água em 6 horas usando 6 ralos. A indústria vai construir um novo reservatório de 500 m³ e quer escoá-lo em 4 horas. Quantos ralos serão necessários?
Resolução:
- Grandezas: Volume, tempo, ralos (incógnita).
- Construção da Tabela:
| Volume (m³) | Tempo (h) | Ralos (Z) |
|---|---|---|
| 900 | 6 | 6 |
| 500 | 4 | Z |
- Análise das Relações:
- Mais volume requer mais ralos (direta).
- Menos tempo requer mais ralos (inversa).
- Montagem da Equação:
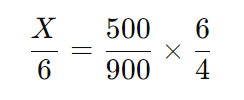
Resolva a equação:

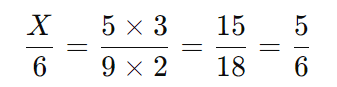
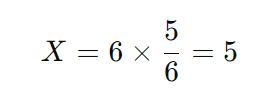
Como o número de ralos precisa ser inteiro, arredondamos para 17 ralos.
Resposta: A indústria precisará de 5 ralos para escoar 500 m³ de água em 4 horas.
Conclusão
A regra de três composta é uma ferramenta poderosa para resolver problemas que envolvem múltiplas grandezas. Entender as relações entre as grandezas e seguir um processo organizado facilita a aplicação desse método em diversas situações do dia a dia e em exames. Pratique com os exemplos e exercícios resolvidos para dominar essa técnica!
Lista de Exercício Regra de Três Composta com gabarito
Exercício 1:
Uma equipe de 8 trabalhadores constrói uma parede em 12 dias. Se a equipe for reduzida para 6 trabalhadores, em quantos dias eles construirão a mesma parede?
a) 10 dias
b) 14 dias
c) 16 dias
d) 18 dias
Exercício 2:
Uma máquina empacota 120 caixas em 5 horas. Quantas horas serão necessárias para que 4 máquinas idênticas empacotem 480 caixas?
a) 2 horas
b) 3 horas
c) 4 horas
d) 5 horas
Exercício 3:
3 pintores pintam 2 paredes em 4 dias. Quantos pintores serão necessários para pintar 6 paredes em 8 dias?
a) 2 pintores
b) 3 pintores
c) 4 pintores
d) 6 pintores
Exercício 4:
Se 10 trabalhadores constroem 15 metros de uma estrada em 5 dias, quantos metros dessa estrada 15 trabalhadores construirão em 10 dias?
a) 30 metros
b) 40 metros
c) 45 metros
d) 50 metros
Exercício 5:
Uma fábrica produz 200 peças em 5 dias, operando 6 horas por dia. Se a fábrica aumentar o tempo de operação para 8 horas por dia, quantas peças serão produzidas em 4 dias?
a) 180 peças
b) 240 peças
c) 320 peças
d) 400 peças
Exercício 6:
Uma torneira enche uma piscina em 15 horas. Se uma segunda torneira idêntica for aberta, quanto tempo levará para encher a piscina?
a) 7,5 horas
b) 10 horas
c) 12 horas
d) 14 horas
Exercício 7:
5 máquinas produzem 500 itens em 4 dias. Quantos itens 10 máquinas produzirão em 2 dias?
a) 250 itens
b) 500 itens
c) 1000 itens
d) 1250 itens
Exercício 8:
Um reservatório de 1000 litros é esvaziado por 5 bombas em 8 horas. Quantas horas levarão 10 bombas para esvaziar um reservatório de 2000 litros?
a) 8 horas
b) 10 horas
c) 12 horas
d) 16 horas
Exercício 9:
12 operários constroem 60 metros de muro em 6 dias. Se o número de operários for reduzido para 8, quantos metros de muro serão construídos em 9 dias?
a) 45 metros
b) 50 metros
c) 55 metros
d) 60 metros
Exercício 10:
Uma máquina empacota 80 caixas em 2 horas. Se o número de máquinas dobrar, quantas caixas serão empacotadas em 3 horas?
a) 120 caixas
b) 240 caixas
c) 320 caixas
d) 480 caixas
Exercício 11:
20 trabalhadores constroem um muro de 30 metros em 15 dias. Quantos trabalhadores serão necessários para construir um muro de 60 metros em 10 dias?
a) 30 trabalhadores
b) 40 trabalhadores
c) 50 trabalhadores
d) 60 trabalhadores
Exercício 12:
6 máquinas produzem 1800 peças em 9 dias. Quantas peças serão produzidas por 8 máquinas em 12 dias?
a) 2400 peças
b) 3200 peças
c) 3600 peças
d) 4800 peças
Exercício 13:
4 impressoras imprimem 1000 páginas em 5 horas. Quantas horas levarão 2 impressoras para imprimir 2000 páginas?
a) 10 horas
b) 15 horas
c) 20 horas
d) 25 horas
Exercício 14:
Se 8 pedreiros constroem 48 metros de uma parede em 6 dias, quantos metros dessa parede 12 pedreiros construirão em 4 dias?
a) 24 metros
b) 36 metros
c) 48 metros
d) 72 metros
Exercício 15:
Uma empresa produz 300 produtos em 3 dias, trabalhando 6 horas por dia. Quantos produtos serão produzidos em 5 dias, se o tempo de trabalho aumentar para 8 horas por dia?
a) 400 produtos
b) 500 produtos
c) 600 produtos
d) 800 produtos
Exercício 16:
Uma fábrica com 5 máquinas operando 10 horas por dia produz 2500 peças em 5 dias. Se o número de máquinas for aumentado para 10, quantas peças serão produzidas em 3 dias, operando 8 horas por dia?
a) 1200 peças
b) 2000 peças
c) 3000 peças
d) 4000 peças
Exercício 17:
Uma equipe de 10 trabalhadores constrói um muro em 20 dias. Se a equipe aumentar para 15 trabalhadores, quantos dias serão necessários para construir o mesmo muro?
a) 10 dias
b) 13 dias
c) 14 dias
d) 15 dias
Exercício 18:
Um grupo de 6 amigos pode encher 300 balões em 2 horas. Quantos balões 4 amigos podem encher em 3 horas?
a) 200 balões
b) 250 balões
c) 300 balões
d) 450 balões
Exercício 19:
Um reservatório de 2000 litros é esvaziado em 4 horas por 4 bombas. Quantas bombas serão necessárias para esvaziar um reservatório de 4000 litros em 2 horas?
a) 8 bombas
b) 10 bombas
c) 12 bombas
d) 16 bombas
Exercício 20:
Uma empresa fabrica 500 peças em 10 dias com 4 máquinas. Quantas peças serão fabricadas em 5 dias se forem usadas 8 máquinas?
a) 250 peças
b) 400 peças
c) 500 peças
d) 800 peças
Gabarito:
- c) 16 dias
- b) 3 horas
- c) 4 pintores
- c) 45 metros
- b) 240 peças
- a) 7,5 horas
- b) 500 itens
- a) 8 horas
- a) 45 metros
- c) 320 caixas
- c) 50 trabalhadores
- c) 3600 peças
- c) 20 horas
- d) 72 metros
- c) 600 produtos
- b) 2000 peças
- d) 15 dias
- b) 250 balões
- c) 12 bombas
- d) 800 peças