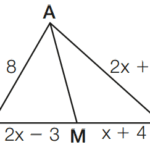A régua é um instrumento que pode ser utilizado no traçado da representação de retas e suas partes.

Vamos marcar dois pontos, A e B, sobre a reta r.

O segmento de reta AB é o conjunto de pontos da reta r compreendidos entre os pontos A e B, incluindo esses dois pontos. Os pontos A e B são chamados extremidades do segmento AB.

Transporte de segmentos
Podemos utilizar o compasso para o transporte de segmentos; acompanhe a construção a seguir. Considere uma reta r e um segmento AB, tal que AB não pertence a r.
Vamos construir sobre r um segmento CD, com o mesmo comprimento de AB, usando o compasso.
1) Traçamos uma reta r e um segmento AB.
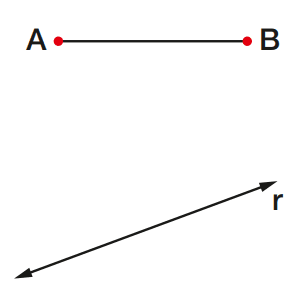
2) Marcamos um ponto C sobre a reta r.
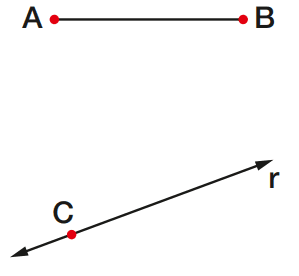
3) Abrimos o compasso, colocando as pontas em A e B.
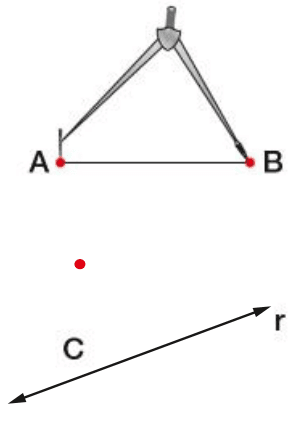
4) Mantendo fixa a abertura do compasso, colocamos a ponta-seca em C e, com a outra ponta, marcamos o ponto D em r.
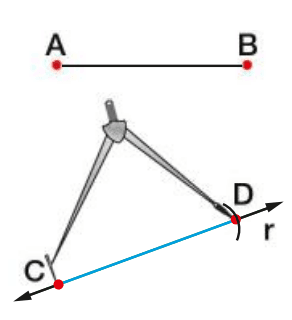
O segmento CD que acabamos de construir tem o mesmo comprimento que AB. Por esse motivo, dizemos que AB e CD são segmentos congruentes.
Congruência de segmentos
Dois segmentos são congruentes quando têm o mesmo comprimento.
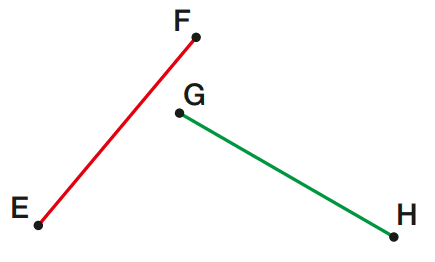
EF e GH têm o mesmo comprimento. Portanto, EF e GH são congruentes. Indicamos:
EF ≡ GH
ê-se: “o segmento EF é congruente ao segmento GH”
Medida de um segmento
Medir um segmento de reta AB significa determinar quantas vezes um segmento unitário padrão (metro, centímetro, milímetro, etc.) cabe no segmento AB. Veja a medida de um segmento AB em centímetro:
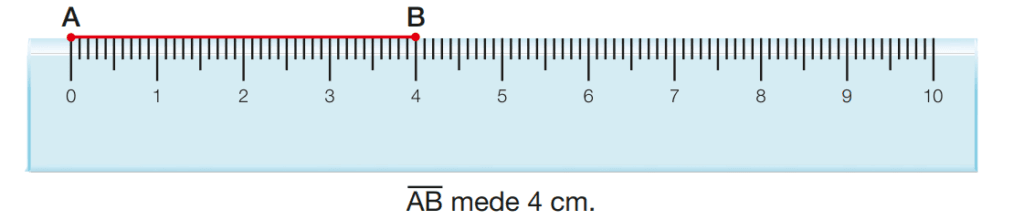
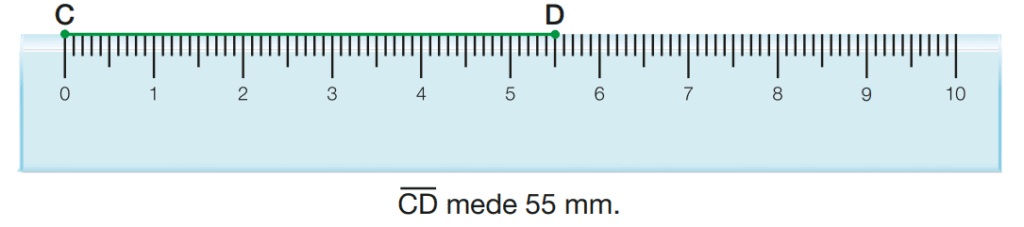
Agora, veja a medida do segmento CD em milímetro:
Dois segmentos são congruentes quando têm medidas iguais
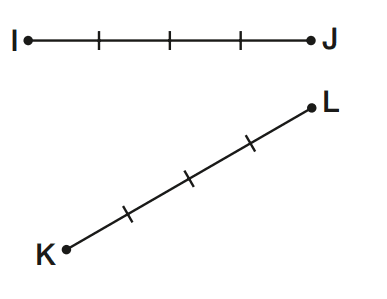
IJ ≡ KL ⇨ (IJ é congruente a KL)
IJ = KL ⇨ (A medida de IJ é igual à medida de KL.)
Ponto médio de um segmento
Observe, na figura, a representação do segmento AB.
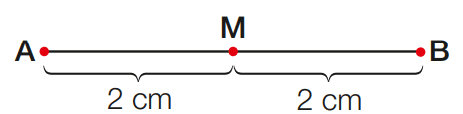
O segmento AB mede 4 cm e o ponto M pertence a ele. Os segmentos AM e MB possuem o mesmo comprimento: 2 cm cada um. Os segmentos AM e MB são congruentes.
Nesse exemplo, M é chamado ponto médio do segmento AB.
Ponto médio de um segmento é um ponto que pertence ao segmento e o divide em dois segmentos congruentes.
Veja como podemos encontrar o ponto médio de um segmento AB usando régua e compasso.
1) Traçamos o segmento AB.

2) Tomamos o compasso com abertura maior que a metade de AB, fixamos a ponta-seca em A e traçamos um arco.
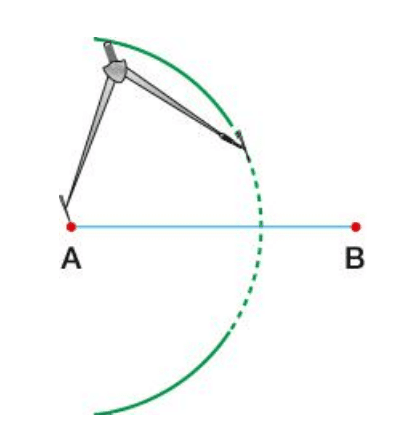
3) Mantendo a abertura do compasso, fixamos a ponta-seca em B e traçamos outro arco. Dessa forma, temos os pontos P e Q, que são as interseções dos arcos.
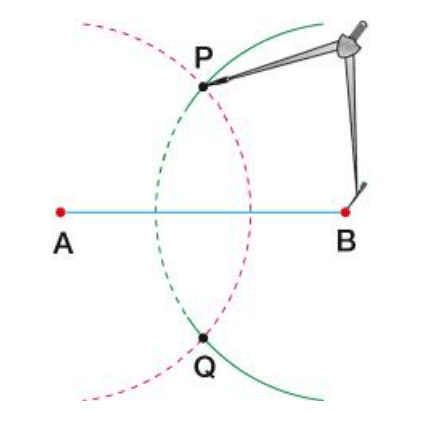
4) Traçamos a reta que une os pontos P e Q e chamamos de M o ponto em que PQ encontra AB.
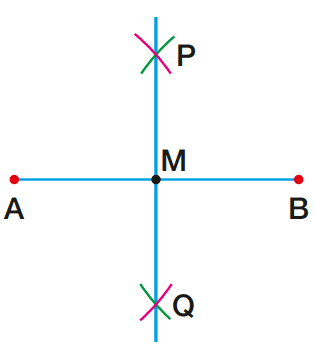
Por construção, P e Q equidistam de A e B. Todo ponto da reta PQ equidista de A e B (como veremos adiante). Então, o ponto M é o ponto médio de AB. A reta PQ é chamada mediatriz de AB.
Exemplo 01: Determine o valor de x e AB, sabendo que M é o ponto médio de AB.
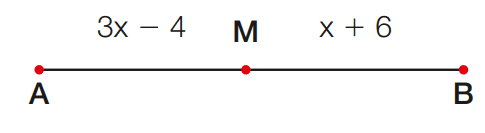
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Solução
3x – 4 = x + 6
3x – x = 6 + 4
2x = 10
x = 10/2
x = 5
AB = 3.5 – 4 + 5 + 6 = 15 – 4 + 5 + 6
AB = 22
[/toggle]
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Leia também…