Dado o sistema de equações

Vamos resolver esse sistema de equações pelo Método de Substituição.
Passo 1: Isolar uma variável
Vamos isolar a variável x na segunda equação:

Passo 2: Substituir a expressão de x nas outras equações
Substituímos a expressão encontrada para x na primeira e na terceira equações.
Substituindo na primeira equação:
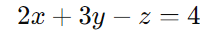
Substituindo x = 6 − y − z:
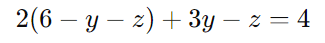
Simplificando:

Substituindo na terceira equação:

Substituindo x = 6 − y − z:
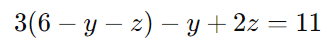
Simplificando:

Passo 3: Substituir e resolver para as variáveis
Agora temos as expressões para y e z em termos das outras variáveis. Substituindo a expressão para y na equação para z:

Resolva essa equação para encontrar z, depois substitua para encontrar x e y.
Vamos continuar a resolução substituindo a expressão de yyy na equação para zzz:
Passo 4: Substituir e Resolver para as Variáveis
Temos:
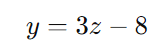
Substituímos y na equação para z:
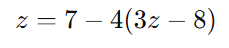
Simplificamos:
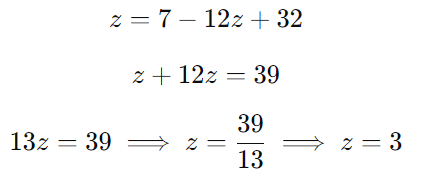
Agora que encontramos o valor de z, podemos substituir para encontrar y:
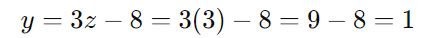
Passo 5: Encontrar x
Substituímos os valores de y e z na expressão para x:
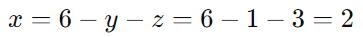
Solução Final
Os valores das variáveis são:
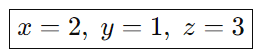
Verificação
Podemos verificar a solução substituindo os valores encontrados nas equações originais:
- Primeira equação:
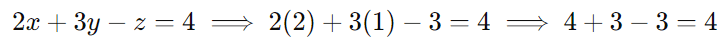
(Está correto.)
- Segunda equação:

(Está correto.)
- Terceira equação:
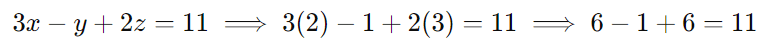
(Está correto.)
A solução está correta: x=2, y=1, z=3.













