(CORREIOS – 2008 – CONSULPLAN )
Numa pesquisa feita sobre um projeto de lei que proíbe a circulação de cães ferozes nas ruas, foram ouvidos 80 moradores de um bairro na cidade de Petrolina/PE. Os resultados encontram-se no quadro abaixo:
Sabe-se que a razão entre o número de pessoas favoráveis ao projeto e o número de pessoas contrárias a ele é 13/7. Qual é o valor de x e y que completam o quadro?
A) x = 8 e y = 12
B) x = 52 e y = 28
C) x = 48 e y = 92
D) x = 12 e y = 28
E) x = 8 e y = 13
Para resolver este problema, devemos usar as informações fornecidas:
Informações principais:
- A razão entre o número de pessoas a favor e o número de pessoas contrárias ao projeto é de 13/7.
- O total de pessoas entrevistadas foi de 80.
Passo a Passo:
- Identificando as variáveis:
- O número total de pessoas favoráveis ao projeto é a soma de homens e mulheres favoráveis, ou seja, ( y + 40 ).
- O número total de pessoas contrárias ao projeto é a soma de homens e mulheres contrários, ou seja, ( 20 + x ).
Usando a razão dada:
A razão entre o número de pessoas favoráveis e o número de pessoas contrárias é de 13/7. Logo, temos:
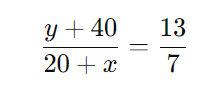
Multiplicando em cruz:
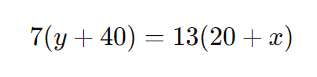
Expandindo ambos os lados:
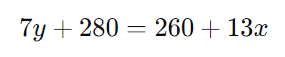
Colocando os termos com variáveis em um lado e os constantes no outro:
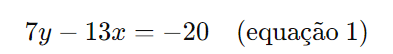
Usando o total de entrevistados:
Sabemos que o total de entrevistados é 80, então:
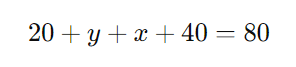
Simplificando:
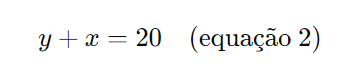
Resolvendo o sistema: A partir da equação 2, temos:
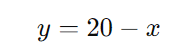
Substituímos esse valor de ( y ) na equação 1:
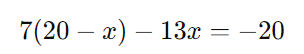
Expandindo:
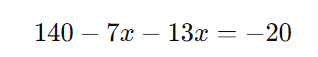
Simplificando:

Isolando ( x ):
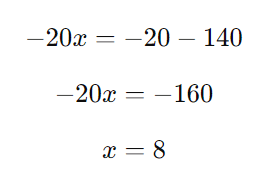
Encontrando ( y ):
Usando a equação ( y = 20 – x ):
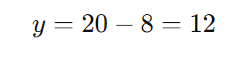
Portanto, os valores de ( x ) e ( y ) que completam o quadro são ( x = 8 ) e ( y = 12 ).
Resposta:
A alternativa correta é A) ( x = 8 ) e ( y = 12 ).













