Quando se fala em finanças, termos como “taxa efetiva” e “taxa real” na matemática financeira são frequentemente mencionados. No entanto, muitas vezes esses conceitos são confundidos ou mal compreendidos. Entender a diferença entre essas taxas e como elas impactam suas decisões financeiras é essencial para gerir bem o seu dinheiro. Neste artigo, vamos explorar o que são a taxa efetiva e a taxa real, como calculá-las e a importância de cada uma.
1. O que é a Taxa Efetiva?
A taxa efetiva é uma medida que reflete o impacto real dos juros compostos ao longo de um período específico. Diferente da taxa nominal, que é a taxa simples anunciada (como 2% ao mês), a taxa efetiva leva em conta a capitalização dos juros — ou seja, como os juros acumulados em um período geram novos juros nos períodos subsequentes.
Exemplo Prático:
Se um investimento oferece 2% de juros ao mês, a taxa efetiva anual não será simplesmente 24% (que é a soma de 2% ao mês ao longo de 12 meses). Considerando o efeito dos juros compostos, a taxa efetiva anual será de aproximadamente 26,82%.
A fórmula para calcular a taxa efetiva é:
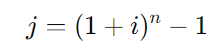
Onde:
- ( j ) é a taxa efetiva,
- ( i ) é a taxa de juros por período (por exemplo, mensal),
- ( n ) é o número de períodos (por exemplo, 12 meses para um cálculo anual).
2. O que é a Taxa Real?
Já a taxa real é um conceito diferente, que ajusta a taxa de juros nominal pela inflação, refletindo o poder de compra real de um investimento ou de uma dívida. A taxa real mostra o quanto o dinheiro realmente cresceu ou foi corroído pela inflação.
Exemplo Prático:
Se um investimento oferece uma taxa nominal de 10% ao ano, mas a inflação no mesmo período foi de 5%, a taxa real será menor, refletindo o ganho real de poder de compra.
A fórmula para calcular a taxa real é:
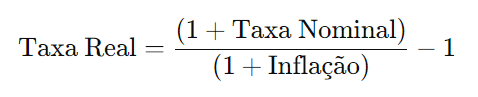
Exemplo de cálculo:
Se a taxa nominal é 10% ao ano e a inflação é 5% ao ano:
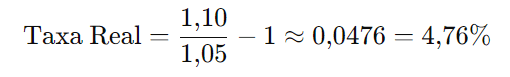
Neste caso, o ganho real, após descontar a inflação, é de aproximadamente 4,76%.
3. Diferenças Entre Taxa Efetiva e Taxa Real
- Finalidade: A taxa efetiva mostra o impacto dos juros compostos ao longo de um período, enquanto a taxa real ajusta a taxa nominal para refletir o impacto da inflação.
- Contexto de Aplicação: A taxa efetiva é usada para entender o custo real de um empréstimo ou o retorno de um investimento, considerando a capitalização dos juros. A taxa real, por outro lado, é usada para avaliar o crescimento real do poder de compra após considerar a inflação.
- Cálculo: A taxa efetiva é calculada com base na capitalização dos juros; a taxa real é calculada ajustando a taxa nominal pela inflação.
4. Importância das Taxas Efetiva e Real nas Finanças Pessoais
Compreender essas taxas é crucial para tomar decisões financeiras informadas:
- Empréstimos: Ao comparar diferentes opções de crédito, a taxa efetiva ajuda a identificar o custo real do empréstimo, enquanto a taxa real ajuda a entender como a inflação pode impactar o valor a ser pago.
- Investimentos: A taxa efetiva mostra o retorno real de um investimento ao considerar os juros compostos, e a taxa real ajusta esse retorno para mostrar o ganho em termos de poder de compra.
- Planejamento Financeiro: Conhecer ambas as taxas permite um planejamento financeiro mais preciso, considerando tanto o impacto dos juros quanto o efeito da inflação.
5. Conclusão
Tanto a taxa efetiva quanto a taxa real são essenciais para uma gestão financeira eficaz. A taxa efetiva oferece uma visão clara do impacto dos juros compostos, enquanto a taxa real ajusta suas expectativas de retorno ou custo ao considerar a inflação. Ao entender e aplicar esses conceitos, você pode tomar decisões financeiras mais informadas, seja ao escolher um empréstimo, um investimento ou ao planejar seu futuro financeiro.
Lembre-se de sempre considerar ambas as taxas em suas análises para garantir que suas escolhas sejam as mais vantajosas possíveis.
Aqui estão quatro exemplos com suas respectivas soluções sobre o cálculo de taxa efetiva e taxa real:
Exemplo 1: Cálculo da Taxa Efetiva Anual a partir de uma Taxa Mensal
Situação: Um banco oferece um empréstimo com uma taxa de juros de 2% ao mês. Qual é a taxa efetiva anual desse empréstimo?
Solução:
A taxa efetiva anual (j) é calculada pela fórmula:
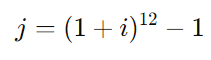
Onde:
- ( i = 0,02 ) (2% ao mês),
- 12 é o número de meses no ano.
Substituindo na fórmula:
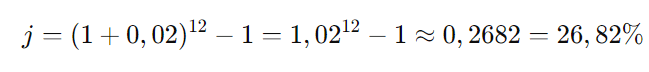
Resposta: A taxa efetiva anual é de aproximadamente 26,82%.
Exemplo 2: Cálculo da Taxa Efetiva Trimestral a partir de uma Taxa Mensal
Situação: Um investimento oferece uma taxa de juros de 1,5% ao mês. Qual é a taxa efetiva trimestral?
Solução:
A taxa efetiva trimestral ((j)) pode ser calculada usando a fórmula:
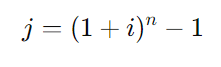
Onde:
- ( i = 0,015 ) (1,5% ao mês),
- ( n = 3 ) (3 meses em um trimestre).
Substituindo na fórmula:
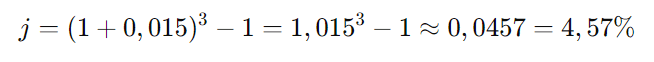
Resposta: A taxa efetiva trimestral é de aproximadamente 4,57%.
Exemplo 3: Cálculo da Taxa Real a partir da Taxa Nominal e da Inflação
Situação: Um investimento oferece uma taxa nominal de 8% ao ano, e a inflação anual é de 3%. Qual é a taxa real desse investimento?
Solução:
A taxa real é calculada pela fórmula:
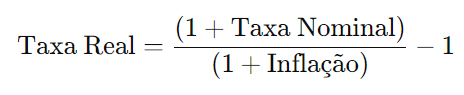
Substituindo os valores:
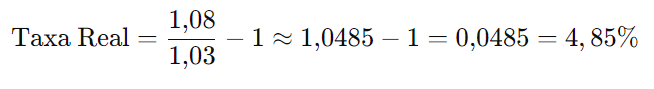
Resposta: A taxa real é de aproximadamente 4,85%.
Exemplo 4: Cálculo da Taxa Real com Alta Inflação
Situação: Um investimento oferece uma taxa nominal de 12% ao ano, mas a inflação anual é de 8%. Qual é a taxa real desse investimento?
Solução:
Usando a fórmula da taxa real:
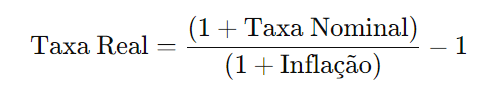
Substituindo os valores:
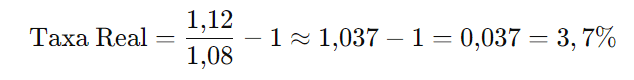
Resposta: A taxa real é de aproximadamente 3,7%.
Esses exemplos demonstram como calcular a taxa efetiva em diferentes períodos e como a inflação pode impactar a taxa real de retorno de um investimento.