No universo financeiro, a compreensão das taxas de juros é fundamental, especialmente quando se trata de tomar decisões relacionadas a empréstimos, financiamentos e investimentos. Duas das taxas mais comuns que surgem nesses contextos da matemática são a taxa nominal e a taxa efetiva. Embora ambas estejam relacionadas ao custo ou ao retorno de uma operação financeira, elas apresentam diferenças significativas, especialmente quando envolvem períodos de capitalização diferentes. Neste artigo, exploraremos a diferença entre taxa nominal e taxa efetiva e aprenderemos como calculá-las.
1. O que é Taxa Nominal?
A taxa nominal é a taxa de juros expressa em uma base anual, sem levar em consideração os períodos de capitalização dentro desse ano. Em outras palavras, a taxa nominal não reflete o efeito dos juros compostos ao longo do tempo. Ela é comumente utilizada em contratos financeiros, como financiamentos e empréstimos, e é a taxa que geralmente aparece nas propagandas de produtos financeiros.
Exemplo de Taxa Nominal:
Se você tem um empréstimo com uma taxa nominal de 12% ao ano, isso significa que, ao longo de um ano, o valor do empréstimo aumenta em 12%, mas isso não necessariamente reflete os juros aplicados mensalmente ou em outros períodos menores de tempo.
2. O que é Taxa Efetiva?
A taxa efetiva, por outro lado, leva em consideração o efeito da capitalização dos juros ao longo do tempo. Ela reflete o custo real ou o retorno real de uma operação financeira, considerando a frequência com que os juros são aplicados (por exemplo, mensalmente, trimestralmente, etc.). Em essência, a taxa efetiva mostra o impacto dos juros compostos sobre o montante total.
A fórmula para calcular a taxa efetiva é:
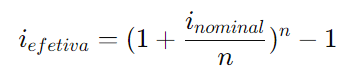
Onde:
- i_{efetiva} é a taxa efetiva,
- i_{nominal} é a taxa nominal,
- n é o número de períodos de capitalização por ano.
3. Diferença entre Taxa Nominal e Taxa Efetiva
A principal diferença entre a taxa nominal e a taxa efetiva é que a taxa nominal não leva em consideração os efeitos da capitalização, enquanto a taxa efetiva reflete o impacto desses juros sobre o valor final. Quanto mais frequente for a capitalização (mensal, trimestral, etc.), maior será a taxa efetiva em relação à taxa nominal.
Exemplo de Diferença:
Se você tem uma taxa nominal de 12% ao ano com capitalização mensal, a taxa efetiva será maior do que 12% devido à aplicação dos juros compostos. Vejamos como calcular isso.
4. Como Calcular a Taxa Efetiva a partir da Taxa Nominal
A seguir, aprenderemos como calcular a taxa efetiva usando a fórmula fornecida anteriormente.
Exemplo Prático:
Suponha que você tenha uma taxa nominal de 12% ao ano e os juros sejam capitalizados mensalmente. Queremos calcular a taxa efetiva anual.
- Taxa Nominal (i_{nominal}) = 12% = 0,12
- Número de períodos de capitalização (n) = 12 (já que os juros são capitalizados mensalmente)
Agora, substituímos esses valores na fórmula:

Portanto, a taxa efetiva anual é de aproximadamente 12,68%, enquanto a taxa nominal é de 12%. Esse acréscimo de 0,68% reflete o efeito dos juros compostos mensais.
5. Como Calcular a Taxa Nominal a partir da Taxa Efetiva
Também é possível fazer o cálculo inverso, ou seja, determinar a taxa nominal a partir da taxa efetiva. A fórmula para isso é a seguinte:
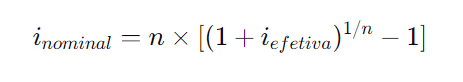
Exemplo Inverso:
Suponha que você tenha uma taxa efetiva de 12,68% ao ano, e os juros sejam capitalizados mensalmente. Queremos descobrir qual seria a taxa nominal correspondente.
- Taxa Efetiva (i_{efetiva}) = 12,68% = 0,126825
- Número de períodos de capitalização (n) = 12 (capitalização mensal)
Substituindo os valores na fórmula:
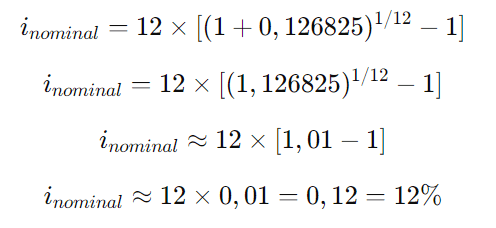
Portanto, a taxa nominal correspondente à taxa efetiva de 12,68% com capitalização mensal é de 12%.
6. Importância de Entender as Taxas de Juros
A compreensão da diferença entre a taxa nominal e a taxa efetiva é essencial para tomar decisões financeiras mais informadas. Alguns pontos importantes a serem considerados:
- Escolha de Financiamentos: Ao comparar diferentes opções de financiamento, é fundamental considerar a taxa efetiva, já que ela reflete o custo real do empréstimo, incluindo o efeito da capitalização dos juros.
- Investimentos: Em aplicações financeiras, a taxa efetiva indica o retorno real sobre o capital investido, especialmente em cenários onde os juros são compostos com frequência.
- Negociações de Contratos: Conhecer a relação entre taxa nominal e efetiva pode ajudar a negociar melhores condições em contratos de empréstimo ou de investimento.
7. Conclusão
A taxa nominal e a taxa efetiva são conceitos essenciais na matemática financeira. Enquanto a taxa nominal é amplamente usada em contratos e anúncios de produtos financeiros, a taxa efetiva reflete o impacto real dos juros compostos ao longo do tempo. Saber como calcular essas taxas e entender sua diferença é fundamental para quem deseja tomar decisões financeiras mais conscientes, seja ao investir, financiar ou avaliar o custo real de uma operação financeira.
Em resumo, ao lidar com operações financeiras, é sempre recomendável prestar atenção à taxa efetiva, pois ela fornece uma visão mais precisa dos custos ou dos ganhos envolvidos, permitindo um planejamento financeiro mais eficaz.













