A área de uma superfície é uma grandeza que representa a extensão de uma região em duas dimensões. Ela é calculada multiplicando-se o comprimento pela largura de uma figura plana. A unidade padrão para medir a área no Sistema Internacional de Unidades (SI) é o metro quadrado (m²).
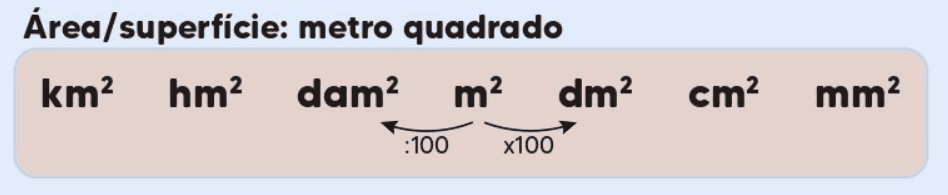
Múltiplos e Submúltiplos do Metro Quadrado
Assim como outras unidades de medida, o metro quadrado possui múltiplos e submúltiplos que são utilizados para medir superfícies maiores ou menores. Esses múltiplos e submúltiplos permitem uma maior precisão e facilidade na representação de áreas muito grandes ou muito pequenas.
Múltiplos do Metro Quadrado
Quilômetro Quadrado (km²):
1 km² = 1.000.000 m²
Utilizado para medir grandes superfícies, como cidades ou regiões.
Hectômetro Quadrado (hm²):
1 hm² = 10.000 m²
Também conhecido como hectare (ha), é comum na agricultura para medir áreas de plantações.
Decâmetro Quadrado (dam²):
1 dam² = 100 m²
Usado para medir áreas um pouco maiores, como parques ou pequenos bairros.
Submúltiplos do Metro Quadrado
Decímetro Quadrado (dm²):
1 dm² = 0,01 m²
Usado para medir superfícies menores, como mesas ou pequenos móveis.
Centímetro Quadrado (cm²):
1 cm² = 0,0001 m²
Comum para áreas muito pequenas, como folhas de papel ou telas de celulares.
Milímetro Quadrado (mm²):
1 mm² = 0,000001 m²
Usado em medições extremamente pequenas, como componentes eletrônicos.
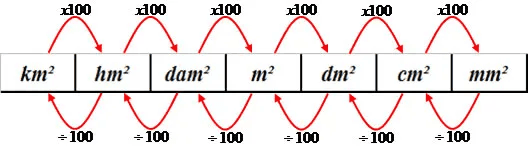
Conversões entre Múltiplos e Submúltiplos
A conversão entre essas unidades de área é feita multiplicando ou dividindo por potências de 10. Por exemplo, para converter 3 km² para m², multiplicamos 3 por 1.000.000, resultando em 3.000.000 m².
Essas unidades de medida e suas conversões são fundamentais em diversas áreas do conhecimento e da prática diária, como na engenharia civil, arquitetura, agricultura, e até na vida cotidiana, ao se determinar o tamanho de um imóvel ou de um terreno.
A Evolução das Unidades de Medida de Área: Uma Jornada pela História
A medição de áreas é uma parte fundamental da nossa vida cotidiana, desde a construção de edifícios e estradas até a simples compra de terrenos e jardinagem. Mas você já parou para pensar sobre a história por trás das unidades de medida de área? Neste artigo, vamos explorar como essas unidades evoluíram ao longo dos séculos e como elas moldaram o mundo em que vivemos hoje.
1. Antiguidade: As Primeiras Medidas
A história das unidades de área começa na Antiguidade, quando civilizações antigas começaram a desenvolver sistemas para medir terrenos e construções.
Egito Antigo:
Os egípcios foram pioneiros na medição de áreas, utilizando unidades baseadas no comprimento, como o “codo” (cubito). Eles introduziram a unidade conhecida como “kite” para medir terrenos e propriedades. O conhecimento matemático avançado dos egípcios foi crucial na construção de pirâmides e na administração de terras agrícolas.
Mesopotâmia:
Na Mesopotâmia, os babilônios usavam a unidade “shet”, derivada do comprimento, para calcular áreas de campos e jardins. Suas técnicas de medição influenciaram profundamente o desenvolvimento da matemática básica e da engenharia.
Grécia Antiga:
Os matemáticos gregos, como Euclides e Arquimedes, fizeram grandes avanços na geometria. Suas descobertas incluíam fórmulas para calcular áreas de formas geométricas, como o triângulo e o círculo, estabelecendo as bases para o entendimento moderno da área.
2. Idade Média: Diversidade de Unidades
Durante a Idade Média, as unidades de medida de área eram muito variadas, refletindo a falta de padronização na época.
Sistema Imperial:
Na Inglaterra medieval, a unidade “acre” era amplamente utilizada para medir terrenos agrícolas. Um acre correspondia a 4.840 jardas quadradas, aproximadamente 4.047 metros quadrados. Esse sistema foi amplamente usado em atividades agrícolas e imobiliárias.
Sistema Métrico:
No final do século XVIII, a Revolução Francesa trouxe uma grande mudança. O sistema métrico foi criado para substituir os diversos sistemas locais e fornecer uma padronização universal. O metro quadrado (m²) foi introduzido como a unidade padrão de área no novo sistema métrico.
3. Era Moderna: Padronização Global
Sistema Internacional de Unidades (SI):
Em 1960, o Sistema Internacional de Unidades (SI) foi oficialmente adotado, estabelecendo o metro quadrado como a unidade padrão global para medir áreas. O SI simplificou a comunicação e a comparação de dados internacionais, promovendo uma padronização que facilita o comércio e a ciência.
Múltiplos e Submúltiplos:
Para lidar com áreas de diferentes magnitudes, foram introduzidos múltiplos e submúltiplos do metro quadrado. Unidades como o quilômetro quadrado (km²) para grandes áreas e o milímetro quadrado (mm²) para áreas muito pequenas tornaram-se comuns, permitindo medições mais precisas e adequadas a diferentes contextos.
Conclusão
A evolução das unidades de medida de área é uma história de inovação e adaptação. Desde os métodos rudimentares das civilizações antigas até o sistema metrificado e padronizado do mundo moderno, cada etapa reflete a necessidade humana de medir e entender o espaço com precisão. Ao reconhecer essa evolução, podemos apreciar melhor a importância dessas unidades na nossa vida cotidiana e como elas moldaram o desenvolvimento da sociedade e da ciência.
Acompanhe nosso blog para mais artigos fascinantes sobre a história e a ciência por trás das unidades de medida e outros temas interessantes!
Exercícios de Unidade de Área e Transformações
1 – Converta 5.000 metros quadrados (m²) para hectares (ha).
2 – Transforme 3,5 quilômetros quadrados (km²) em metros quadrados (m²).
3 – Converta 2.500 centímetros quadrados (cm²) para metros quadrados (m²).
4 – Calcule a área de um retângulo com comprimento de 12 metros e largura de 8 metros.
5 – Determine a área de um triângulo com base de 10 metros e altura de 6 metros.
6 – Encontre a área de um círculo com raio de 7 metros. (Use π ≈ 3,14)
7 – Um terreno retangular possui 50 metros de comprimento e 30 metros de largura. Qual é a área total do terreno em hectares?
8 – Um campo de futebol tem uma área de 0,5 hectares. Converta essa área para metros quadrados.
9 – Um jardineiro deseja cobrir um jardim de 200 m² com plantas. Quantos metros quadrados de plantas ele precisará se cada pacote de plantas cobre 10 m²?
10 – Se um lote tem 250.000 cm², qual é a sua área em metros quadrados?
11 – Converta uma área de 1.200 decímetros quadrados (dm²) para metros quadrados (m²).
12 – Um edifício ocupa uma área de 3 km². Quantos hectares isso representa?
13 – Um terreno é composto por um retângulo de 20 metros por 15 metros e um triângulo de base 10 metros e altura 5 metros. Qual é a área total do terreno?
14 – Calcule a área de um quadrado cuja diagonal mede 10 metros.
15 – Um campo é dividido em duas partes iguais: uma parte retangular com dimensões 25 metros por 12 metros e outra parte circular com raio de 10 metros. Qual é a área total do campo?
16 – Um edifício tem uma fachada com a forma de um trapézio com bases de 30 metros e 20 metros e altura de 12 metros. Qual é a área da fachada?
17 – Converta a área de um círculo de 5 km de raio para centímetros quadrados.
18 – Se um terreno tem uma área de 2.000.000 mm², qual é a área em metros quadrados?
Gabarito
- Converta 5.000 metros quadrados (m²) para hectares (ha).
5.000 m² = 0,5 ha - Transforme 3,5 quilômetros quadrados (km²) em metros quadrados (m²).
3,5 km² = 3.500.000 m² - Converta 2.500 centímetros quadrados (cm²) para metros quadrados (m²).
2.500 cm² = 0,25 m² - Calcule a área de um retângulo com comprimento de 12 metros e largura de 8 metros.
Área = 12 m × 8 m = 96 m² - Determine a área de um triângulo com base de 10 metros e altura de 6 metros.
Área = (10 m × 6 m) / 2 = 30 m² - Encontre a área de um círculo com raio de 7 metros. (Use π ≈ 3,14)
Área = π × 7² ≈ 3,14 × 49 ≈ 153,86 m² - Um terreno retangular possui 50 metros de comprimento e 30 metros de largura. Qual é a área total do terreno em hectares?
Área = 50 m × 30 m = 1.500 m²
1.500 m² = 0,15 ha - Um campo de futebol tem uma área de 0,5 hectares. Converta essa área para metros quadrados.
0,5 ha = 5.000 m² - Um jardineiro deseja cobrir um jardim de 200 m² com plantas. Quantos metros quadrados de plantas ele precisará se cada pacote de plantas cobre 10 m²?
Número de pacotes = 200 m² / 10 m² = 20 pacotes - Se um lote tem 250.000 cm², qual é a sua área em metros quadrados?
250.000 cm² = 25 m² - Converta uma área de 1.200 decímetros quadrados (dm²) para metros quadrados (m²).
1.200 dm² = 12 m² - Um edifício ocupa uma área de 3 km². Quantos hectares isso representa?
3 km² = 300 ha - Um terreno é composto por um retângulo de 20 metros por 15 metros e um triângulo de base 10 metros e altura 5 metros. Qual é a área total do terreno?
Área do retângulo = 20 m × 15 m = 300 m²
Área do triângulo = (10 m × 5 m) / 2 = 25 m²
Área total = 300 m² + 25 m² = 325 m² - Calcule a área de um quadrado cuja diagonal mede 10 metros.
Área = (diagonal²) / 2
Área = (10 m)² / 2 = 50 m² - Um campo é dividido em duas partes iguais: uma parte retangular com dimensões 25 metros por 12 metros e outra parte circular com raio de 10 metros. Qual é a área total do campo?
Área da parte retangular = 25 m × 12 m = 300 m²
Área da parte circular = π × 10² ≈ 3,14 × 100 = 314 m²
Área total = 300 m² + 314 m² = 614 m² - Um edifício tem uma fachada com a forma de um trapézio com bases de 30 metros e 20 metros e altura de 12 metros. Qual é a área da fachada?
Área = ((Base maior + Base menor) × Altura) / 2
Área = ((30 m + 20 m) × 12 m) / 2 = 300 m² - Converta a área de um círculo de 5 km de raio para centímetros quadrados.
Área = π × 5² km² = 25π km²
25π km² = 25 × 3,14 × (1.000.000 m²) = 78.539.816,34 cm² - Se um terreno tem uma área de 2.000.000 mm², qual é a área em metros quadrados?
2.000.000 mm² = 2 m²
Leia também
Unidade de Medida e Transformação: Comprimento (Metro m)
Unidade de Medida e Transformação: Área (Metro Quadrado m²)