Unidade de Medida – Matemática CESPE – Concurso Público

(CESPE / CEBRASPE 2019 – TJ-PR – Técnico Judiciário)

Mesmo com a informatização dos processos, ainda é grande o volume de papéis consumidos nas instituições públicas, o que demanda grandes espaços para seu armazenamento. Por exemplo, uma caixa na forma de um paralelepípedo retângulo medindo 31 cm de largura, 25 cm de altura e 42 cm de comprimento armazena 10 resmas de papel A4. Nesse caso, para armazenar 1.000 dessas caixas em um contêiner, é necessário que a capacidade desse contêiner seja de

A) 32,55 m³ .
B) 39,20 m³ .
C) 77,50 m³ .
D) 98 m³.
E) 105 m³ .

Solução em vídeo

Para resolver este problema, precisamos calcular o volume de uma única caixa e depois multiplicar esse volume pelo número de caixas que precisam ser armazenadas (1.000 caixas).

Passo 1: Cálculo do volume da caixa

A caixa é um paralelepípedo retangular com as seguintes dimensões:

• Largura: 31 cm
• Altura: 25 cm
• Comprimento: 42 cm

O volume ( V ) de um paralelepípedo é dado pela fórmula:

V = largura x altura x comprimento

Substituindo os valores:

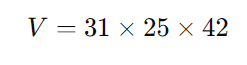
Vamos calcular esse valor:

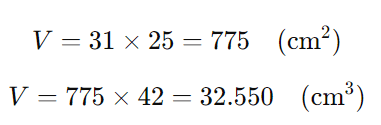
O volume de uma caixa é de 32.550 cm³.

Passo 2: Conversão de centímetros cúbicos para metros cúbicos

Como 1 metro cúbico (m³) é igual a 1.000.000 centímetros cúbicos (cm³), podemos converter o volume da caixa para metros cúbicos:

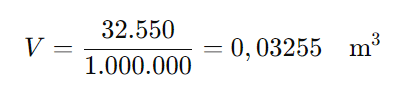
Passo 3: Cálculo do volume necessário para 1.000 caixas

Para armazenar 1.000 caixas, precisamos multiplicar o volume de uma única caixa pelo número total de caixas:

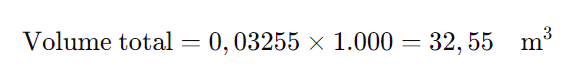
Conclusão

A capacidade do contêiner deve ser de 32,55 m³. Portanto, a alternativa correta é:

A) 32,55 m³.