A probabilidade é um ramo essencial da Matemática que nos permite lidar com situações de incerteza de forma lógica e estruturada. Desde jogos de azar até decisões médicas e estatísticas, o conceito de chance está presente em nosso cotidiano.
Esta lista de exercícios foi cuidadosamente elaborada para desenvolver o raciocínio lógico, a interpretação de problemas e a habilidade de cálculo envolvendo eventos aleatórios. Ao resolver as questões, você terá a oportunidade de praticar desde os conceitos mais básicos — como espaço amostral e eventos equiprováveis — até aplicações mais contextualizadas, como problemas do ENEM e concursos públicos.
01. No lançamento simultâneo de dois dados honestos, determine a probabilidade de obtermos:
a) A soma das faces viradas para cima igual a 7;
b) Uma face virada para cima igual a 1 e outra igual a 4.
c) A soma das faces viradas para cima maior que 9.
Ver Solução
Espaço amostral total (E):
Dois dados honestos → 6×6=36 possíveis combinações.
a) Soma igual a 7:
Combinações: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1)
→ 6 casos favoráveis P = 6/36 =1/6
b) Uma face 1 e outra 4:
Casos: (1,4) e (4,1) → 2 casos favoráveis P = 2/36 = 1/18
c) Soma maior que 9:
Somas possíveis: 10, 11 ou 12
→ (4,6), (5,5), (6,4), (5,6), (6,5), (6,6) = 6 casos P = 6/36 = 1/6
Resumo:
a) 1/6
b) 1/18
c) 1/6
02. Em uma moeda viciada a probabilidade de sair cara é igual ao triplo de sair coroa. Determine a probabilidade de, no lançamento dessa moeda, obtermos cara.
Ver Solução
Seja P(C) a probabilidade de sair coroa.
Então, P(K) = 3⋅P(C), onde K representa cara.
Sabemos que a soma das probabilidades deve ser 1: P(C) + P(K) = 1 ⇒ P(C) + 3P(C) = 1 ⇒ 4P(C) = 1 ⇒ P(C) = 1/4
Logo, P(K) = 3⋅1/4 = 3/4
Resposta: 3/4
03. Em uma urna existem 10 bolas numeradas de 1 a 10. Sorteando-se aleatoriamente 3 bolas, qual é a probabilidade de a bola de número 5 estar entre as bolas sorteadas?
Ver Solução
Escolher 3 bolas entre 10 → combinação:
Casos favoráveis:
Queremos que a bola número 5 esteja entre as sorteadas.
Fixando a bola 5, restam 2 posições a serem preenchidas com as outras 9 bolas (exceto a 5):
Probabilidade: P = 36/120 = 3/10
Resposta: 3/10
04. Uma urna contém 5 bolas azuis e 6 bolas pretas. Na retirada simultânea de 3 bolas, determine a probabilidade de:
a) Retirarmos 3 bolas pretas;
b) Retirarmos 3 bolas azuis;
c) Retirarmos pelo menos 1 bola preta.
Ver Solução
Total de bolas:
5 azuis + 6 pretas = 11 bolas
Espaço amostral (total de maneiras de escolher 3 bolas):
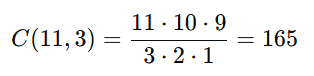
a) Três bolas pretas:
Escolher 3 entre 6 pretas:
b) Três bolas azuis:
Escolher 3 entre 5 azuis:
c) Pelo menos uma bola preta:
Mais fácil calcular o complementar: nenhuma preta → todas azuis.
Total de maneiras de tirar 3 azuis (já feito):
C(5,3) = 10
Logo:
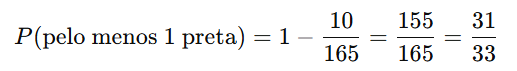
Respostas:
a) 4/33
b) 2/33
c) 31/33
05. (Eear 2017) Uma urna contém bolas verdes e azuis. Sabe-se que a probabilidade de se retirar uma bola azul é de 6/11. A probabilidade de ser retirada, em uma única tentativa, uma bola verde é de
a) 1/11 b) 2/11 c) 4/11 d) 5/11
Ver Solução
Se a probabilidade de retirar uma bola azul é 6/11, e sabendo que só existem bolas verdes e azuis na urna, então:
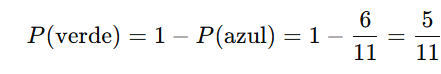
Resposta correta: Letra d) 5/11
06. (Fmp 2017) Um grupo é formado por três homens e duas mulheres. Foram escolhidas, ao acaso, três pessoas desse grupo. Qual é a probabilidade de as duas mulheres do grupo estarem entre as três pessoas escolhidas?
a) 3/10 b) 1/10 c) 2/5 d) 2/3 e) 1/3
Ver Solução
Total de pessoas:
3 homens + 2 mulheres = 5 pessoas
Total de maneiras de escolher 3 pessoas:
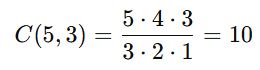
Casos favoráveis: queremos que as 2 mulheres estejam incluídas.
Ou seja, fixamos as 2 mulheres e escolhemos 1 homem dentre os 3 disponíveis: C(3,1) = 3
Probabilidade: P =3/10
Resposta correta: Letra a) 3/10
07. (Unisc 2016) Dentre um grupo formado por 2 Engenheiros e 4 Matemáticos, três pessoas são escolhidas ao acaso. A probabilidade de que sejam escolhidos um Engenheiro e dois Matemáticos é de:
a) 25% b) 35% c) 39% d) 50% e) 60%
Ver Solução
Total de pessoas:
2 engenheiros + 4 matemáticos = 6 pessoas
Espaço amostral:
Número total de maneiras de escolher 3 pessoas entre as 6:
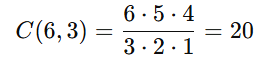
Casos favoráveis:
Queremos 1 engenheiro (entre 2) e 2 matemáticos (entre 4):
Probabilidade:
Resposta correta: Letra e) 60%
08. (Upf 2016) Um pescador pescou 10 peixes, dos quais 3 tinham um tamanho inferior ao permitido pela lei. Esse pescador foi abordado por um fiscal que, dentre os 10 peixes, resolveu inspecionar apenas 2, escolhendo-os aleatoriamente. A probabilidade de o pescador não ser flagrado infringindo a lei é de:
a) 7/10 b) 7/15 c) 3/100 d) 13/45 e) 9/100
Ver Solução
Total de peixes: 10
Peixes irregulares: 3
Peixes regulares: 7
Queremos a probabilidade de o fiscal não pegar nenhum peixe irregular, ou seja, os 2 peixes sorteados são regulares.
Total de maneiras de escolher 2 peixes entre os 10:
Casos favoráveis: escolher 2 entre os 7 regulares:
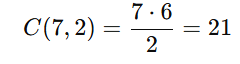
Probabilidade:
Resposta correta: Letra b) 7/15
09. (Ueg 2016) Pedro jogou dois dados comuns numerados de 1 a 6. Sabendo-se que o produto dos números sorteados nos dois dados é múltiplo de 3, a probabilidade de terem sido sorteados os números 3 e 4 é uma em
a) 18 b) 12 c) 10 d) 9
Ver Solução
- Espaço total: 6 × 6 = 36 pares possíveis.
- Produto múltiplo de 3: basta que um dos números seja 3 ou 6.
- Contando as combinações com pelo menos um número múltiplo de 3: 10 pares válidos, entre eles (3,1), (3,2), …, (3,6), (1,3), (2,3), (4,3), (5,3) — total de 10.
- Caso favorável: apenas (3,4) satisfaz a condição e a pergunta → 1 caso.
Resposta correta: letra c)
10. (Pucrj 2016) Temos um baralho comum, com 52 cartas, das quais 4 são ases.
a) Tiramos uma carta ao acaso. Qual é a probabilidade de que ela seja um ás?
b) Tiramos (do baralho completo) 5 cartas (simultaneamente). Qual é a probabilidade de que, entre essas cartas, não haja nenhum ás?
Ver Solução
Letra a)
Total de cartas: 52
Número de ases:
Letra b)
Queremos a probabilidade de não sair nenhum ás ao tirar 5 cartas.
Total de formas de escolher 5 cartas do baralho: C(52,5)
Número de formas de escolher 5 cartas sem ases:
Como há 48 cartas que não são ases: C(48,5)
Probabilidade:
Calculando valores:
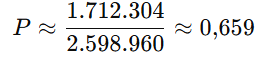
Resposta final:
a) 1/13
b) Aproximadamente 0,659 ou 65,9%
11. (Enem 2015) Em uma central de atendimento, cem pessoas receberam senhas numeradas de 1 até 100. Uma das senhas é sorteada ao acaso.
Qual é a probabilidade de a senha sorteada ser um número de 1 a 20?
a) 1/100 b) 19/100 c) 20/100 d) 21/100 e) 80/100
Ver Solução
Total de senhas: 100
Senhas desejadas (de 1 a 20): 20
Resposta correta: Letra c) 20/100
12. (Enem 2014) Para analisar o desempenho de um método diagnóstico, realizaram-se estudos em populações contendo pacientes sadios e doentes. Quatro situações distintas podem acontecer nesse contexto de teste:
- Paciente TEM a doença e o resultado do teste é POSITIVO.
- Paciente TEM a doença e o resultado do teste é NEGATIVO.
- Paciente NÃO TEM a doença e o resultado do teste é POSITIVO.
- Paciente NÃO TEM a doença e o resultado do teste é NEGATIVO.
Um índice de desempenho para avaliação de um teste diagnóstico é a sensibilidade, definida como a probabilidade de o resultado do teste ser POSITIVO se o paciente estiver com a doença. O quadro refere-se a um teste diagnóstico para a doença A, aplicado em uma amostra composta por duzentos indivíduos.
Conforme o quadro do teste proposto, a
sensibilidade dele é de
a) 47,5%
b) 85,0%
c) 86,3%
d) 94,4%
e) 95,0%
Ver Solução
A sensibilidade é a probabilidade de o teste dar positivo quando a pessoa realmente tem a doença, ou seja:
- Doentes (Doença A Presente):
- Teste Positivo = 95 (Verdadeiros Positivos)
- Teste Negativo = 5 (Falsos Negativos)
- Total de doentes = 95 + 5 = 100
🧮 Cálculo:
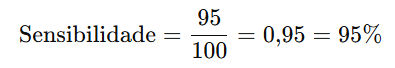
Resposta correta: ✅ letra e) 95,0%
13. (Enem 2011) Rafael mora no Centro de uma cidade e decidiu se mudar, por recomendações médicas, para uma das regiões: Rural, Comercial, Residencial Urbano ou Residencial Suburbano. A principal recomendação médica foi com as temperaturas das “ilhas de calor” da região, que deveriam ser inferiores a 31 °C. Tais temperaturas são apresentadas no gráfico:
Escolhendo, aleatoriamente, uma das outras regiões para morar, a probabilidade de ele escolher uma região que seja adequada às recomendações médicas é
a) 1/5 b) 1/4 c) 2/5 d) 3/5 e) 3/4
Ver Solução
Das 4 regiões disponíveis (Rural, Comercial, Residencial Urbana e Residencial Suburbana), as que apresentam temperatura inferior a 31 °C, conforme o gráfico, são:
- Rural
- Residencial Urbana
- Residencial Suburbana
Logo, há 3 regiões adequadas em 4 possíveis:
P = 3/4
✅ Resposta: letra e)
14. (Enem 2006) A tabela a seguir indica a posição relativa de quatro times de futebol na classificação geral de um torneio, em dois anos consecutivos. O símbolo • significa que o time indicado na linha ficou, no ano de 2004, à frente do indicado na coluna. O símbolo * significa que o time indicado na linha ficou, no ano de 2005, à frente do indicado na coluna.
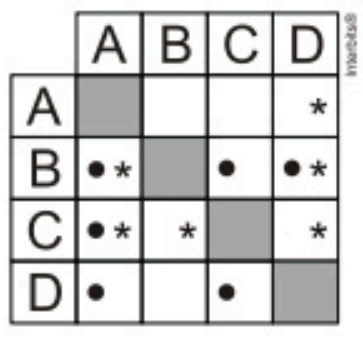
A probabilidade de que um desses quatro times, escolhido ao acaso, tenha obtido a mesma classificação no torneio em 2004 e 2005 é igual a
a) 0,00 b) 0,25 c) 0,50 d) 0,75 e) 1,00
Ver Solução
🧠 Enunciado resumido:
Queremos saber quantos dos 4 times (A, B, C, D) tiveram a mesma posição nos dois anos (2004 e 2005).
- ● → ficou à frente em 2004
- → ficou à frente em 2005
📊 Análise por time:
🔹 Time A:
- 2004: ficou à frente de B, C e D → 1º lugar
- 2005: só à frente de D → não manteve posição
❌ Não teve mesma posição
🔹 Time B:
- 2004: atrás de A, à frente de C e D → 2º
- 2005: à frente de C e D → 2º
✅ Manteve a posição
🔹 Time C:
- 2004: atrás de A e B, à frente de D → 3º
- 2005: atrás de B, à frente de D → 3º
✅ Manteve a posição
🔹 Time D:
- 2004: último
- 2005: último
✅ Manteve a posição
✅ Total de times com mesma classificação nos dois anos:
3 times (B, C, D)
🎯 Probabilidade:
P = 3/4 = 0,75
✅ Resposta correta: letra d) 0,75
15. No plano cartesiano, uma partícula se move nos seguintes movimentos: “de baixo para cima” (↑) ou “da esquerda para a direita” (→). Tomando o ponto O(0, 0) como origem (saída), qual a probabilidade dessa partícula chegar ao ponto A(4, 5), passando pelo ponto (1, 2), considerando todos os possíveis caminhos?
Ver Solução
- Total de caminhos de (0,0)até (4,5)
→ 4 passos → e 5 passos ↑ →
- Caminhos que passam por (1,2):
1. De (0,0) até (1,2): 1 passo →, 2 passos ↑ →
C(3, 1)=3
2. De (1,2) até (4,5): 3 passos →, 3 passos ↑ →
C(6, 3)=20
Caminhos passando por (1,2) = 3×20 = 60
🎯 Probabilidade pedida:
✅ Resposta correta: 10/21
16. Considerando todos os anagramas que podemos formar da palavra BOTAFOGO, determine a probabilidade de termos:
a) As vogais juntas.
b) As consoantes em ordem alfabética.
Ver Solução
Palavra: BOTAFOGO
- Total de letras: 8
- Letra O se repete 3 vezes
- Total de anagramas possíveis:
8!/3! = 6720
a) Vogais juntas (O, O, O, A)
- Agrupamos as vogais como um bloco → 5 blocos no total (4 consoantes + 1 bloco de vogais)
- Permutação dos blocos: 5! = 120
- Permutação das vogais: 4!/3! = 4
Total favorável=120×4 = 480 ⇒
P = 480/6720 = 1/14
b) Consoantes em ordem alfabética (B, F, G, T)
- Fixamos essas 4 consoantes em ordem nas 8 posições → C(8, 4) = 70
- As vogais restantes (O, O, O, A) se permutam: 4!/3! = 4
Total favorável = 70×4 = 280 ⇒
P=280/6720 = 1/24
✅ Respostas:
- a) 1/14 ou 7,14%
- b) 1/24 ou 4,16%
17. Seja A={ 1/4, 1/2, 1, 2, 4, 8} e B={ 1/3, 1, 3, 9, 27}.
Substituindo, aleatoriamente, um elemento de A em x e um elemento de B em y, determine a probabilidade de logyx>0, supondo que exista.
Ver Solução
- Total de pares possíveis: 6×5=306 \times 5 = 306×5=30
- Casos favoráveis:
• x > 1 e y > 1: 3×3 = 9
• 0 < x < 1 e 0 < y < 1: 2×1 = 2 - ➡️ Total de casos favoráveis: 9+2 = 11
→ Total: 11 casos
🔢 Total de casos possíveis:
6 elementos em A×5 elementos em B = 30
✅ Probabilidade de logyx>0:
11/30
