Domine o Teorema de Tales e o conceito de razão e proporcionalidade com estes 7 exercícios resolvidos passo a passo.
Nesta seleção, você encontrará problemas com figuras, situações cotidianas, conversão de temperaturas, uso de segmentos proporcionais e análise de dados.
Tudo foi elaborado com explicações claras, imagens, fórmulas matemáticas em LaTeX (MathJax) e botão de abre/fecha para a solução, ideal para revisar e aprender com autonomia.
Ao final de cada exercício, você também pode acessar gratuitamente nossos mapas mentais e os 10 eBooks de Matemática.
✅ Ideal para alunos do Ensino Fundamental II e Médio
📘 Material perfeito para reforço escolar e preparação para provas
Exercícios sobre Teorema de Tales
Exercício 1
Uma pessoa tem 1,95 m de altura e, em determinado instante, sua sombra mede 2,60 m. Calcule a razão entre a medida da altura da pessoa e a medida de sua sombra naquele instante.
👇 Ver solução passo a passo
Passo 1: Identificar os dados:
- Altura da pessoa: \( 1{,}95 \, \text{m} \)
- Comprimento da sombra: \( 2{,}60 \, \text{m} \)
Passo 2: Calcular a razão entre altura e sombra:
\( \frac{1{,}95}{2{,}60} \)
Multiplicando numerador e denominador por 100 para eliminar as casas decimais:
\( \frac{195}{260} \)
Agora simplificando a fração (dividindo por 65):
\( \frac{195 \div 65}{260 \div 65} = \frac{3}{4} \)
Resposta final: A razão entre a altura e a sombra é \( \boxed{\frac{3}{4}} \).
🔗 Material complementar gratuito
Exercício 2
Na figura a seguir, as retas \( r, s, t \) e \( u \) são paralelas. Com as informações fornecidas, deseja-se calcular as medidas \( x \) e \( y \) indicadas.
a) A partir das informações dadas, é possível resolver o problema?
b) Se for possível, resolva o problema. Se não for possível, indique quais informações estão faltando para que as medidas possam ser encontradas.
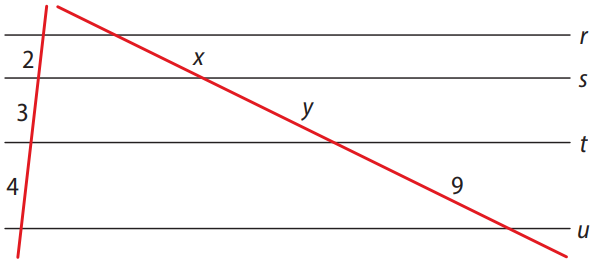
👇 Ver solução passo a passo
Sim, é possível resolver o problema usando o Teorema de Tales, pois temos um feixe de retas paralelas cortado por uma transversal.
Passo 1: Aplicando o Teorema de Tales, com base nas distâncias verticais e nos segmentos horizontais:
\[ \frac{x}{2} = \frac{y}{3} = \frac{9}{4} \]
Passo 2: Igualando \( \frac{x}{2} = \frac{9}{4} \):
\( x = \frac{2 \cdot 9}{4} = \frac{18}{4} = 4{,}5 \)
Passo 3: Igualando \( \frac{y}{3} = \frac{9}{4} \):
\( y = \frac{3 \cdot 9}{4} = \frac{27}{4} = 6{,}75 \)
Resposta final: \( x = 4{,}5 \, \text{cm} \), \( y = 6{,}75 \, \text{cm} \)
🔗 Material complementar gratuito
Exercício 3
Duas avenidas se encontram em um ponto \( A \). Essas avenidas intersectam três ruas, \( r_1, r_2 \) e \( r_3 \), que são paralelas entre si. Os segmentos de reta \( \overline{AD}, \overline{AB} \) e \( \overline{BC} \) representam quarteirões da avenida 2.
Na figura, estão indicados os comprimentos, em metros, de alguns quarteirões. Determine os comprimentos dos quarteirões representados pelos segmentos de reta \( \overline{BC} \) e \( \overline{AM} \).
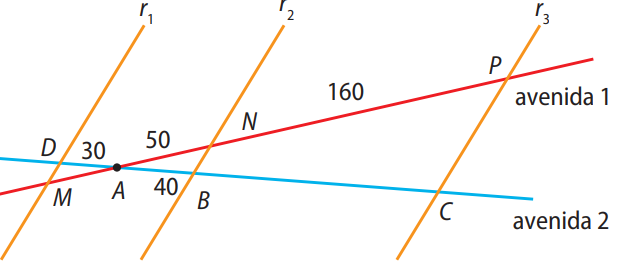
👇 Ver solução passo a passo
Passo 1: Aplicando o Teorema de Tales nas retas paralelas \( r_1, r_2, r_3 \), com os segmentos sobre a avenida 1:
\( \frac{AD}{AB} = \frac{MP}{BC} \)
Como:
- \( AD = 30\,m \)
- \( AB = 30 + 50 = 80\,m \)
- \( MP = 160\,m \)
Substituindo na proporção:
\( \frac{30}{80} = \frac{160}{BC} \Rightarrow BC = \frac{160 \cdot 80}{30} = \frac{12800}{30} = \boxed{128\,m} \)
Passo 2: Agora, aplicando a mesma proporção para encontrar \( AM \):
\( \frac{AM}{AD} = \frac{MP}{AB} \Rightarrow \frac{AM}{30} = \frac{160}{80} = 2 \Rightarrow AM = 2 \cdot 15 = \boxed{37{,}5\,m} \)
Resposta final:
- \( \overline{BC} = 128\,m \)
- \( \overline{AM} = 37{,}5\,m \)
🔗 Material complementar gratuito
Exercício 4
Considerando que \( \overline{AB}, \overline{CD}, \overline{MN} \) e \( \overline{PQ} \) são proporcionais nessa ordem e sabendo que:
- \( AB = (x + 3)\, \text{cm} \)
- \( CD = (x – 2)\, \text{cm} \)
- \( MN = 40\, \text{cm} \)
- \( PQ = 30\, \text{cm} \)
Calcule as medidas dos segmentos \( \overline{AB} \) e \( \overline{CD} \).
👇 Ver solução passo a passo
Passo 1: Montar a proporção entre os segmentos, conforme a ordem dada:
\[ \frac{x + 3}{x – 2} = \frac{40}{30} \]
Passo 2: Simplificar a razão numérica:
\( \frac{40}{30} = \frac{4}{3} \)
Passo 3: Resolver a proporção por multiplicação cruzada:
\( 3(x + 3) = 4(x – 2) \)
Distribuindo os dois lados:
\( 3x + 9 = 4x – 8 \)
Isolando \( x \):
\( 17 = x \)
Passo 4: Calcular os segmentos:
- \( AB = x + 3 = 17 + 3 = \boxed{20\,\text{cm}} \)
- \( CD = x – 2 = 17 – 2 = \boxed{15\,\text{cm}} \)
Resposta final: \( AB = 20\,\text{cm}, \quad CD = 15\,\text{cm} \)
🔗 Material complementar gratuito
Exercício 5
Observe a figura a seguir, em que as retas \( a, b \) e \( c \) são paralelas, e as medidas estão em centímetros. Deseja-se determinar as medidas dos segmentos \( \overline{DE} \) e \( \overline{EF} \).
a) A partir das informações dadas, é possível resolver o problema?
b) Se for possível, resolva o problema. Se não for possível, indique quais informações estão faltando para que as medidas possam ser encontradas.
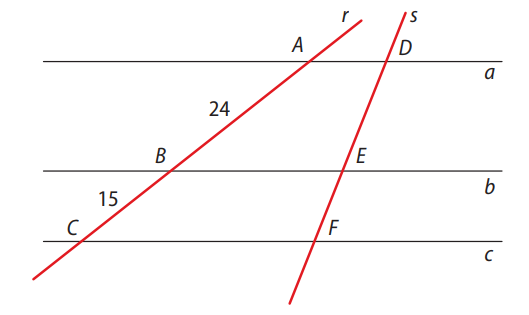
👇 Ver análise e justificativa
Resposta da letra (a): Não.
Justificativa:
O Teorema de Tales exige que as proporções sejam feitas entre segmentos correspondentes de duas transversais que cruzam um feixe de retas paralelas. Na figura, temos as retas \( a \), \( b \) e \( c \) paralelas, mas as transversais \( r \) e \( s \) não têm todos os seus segmentos medidos.
Apenas temos os comprimentos de \( \overline{AB} = 24\,\text{cm} \) e \( \overline{BC} = 15\,\text{cm} \), mas falta o valor total de \( \overline{AC} \), e principalmente, não temos nenhuma medida nos segmentos da outra transversal (\( \overline{DE}, \overline{EF} \)) que permita montar uma proporção.
Resposta da letra (b):
Para que o problema possa ser resolvido, seria necessário conhecer, por exemplo:
- O comprimento de \( \overline{DF} \) na transversal \( s \);
- Ou o valor de \( \overline{DE} \) ou \( \overline{EF} \) separadamente;
- Ou ainda a razão entre os lados da transversal \( s \) que tornaria possível aplicar o Teorema de Tales.
Conclusão: Com os dados apresentados, não é possível resolver o problema.
🔗 Material complementar gratuito
Exercício 6
Os segmentos \( \overline{AB}, \overline{CD}, \overline{EF} \) e \( \overline{GH} \) são proporcionais. A soma das medidas dos dois primeiros segmentos equivale a 12, e a diferença entre essas medidas é igual a 2. Com relação aos dois últimos segmentos, sabemos que a medida do primeiro é o triplo da medida do segundo menos duas unidades.
Nessas condições, determine a soma das medidas de todos os segmentos.
👇 Ver solução passo a passo
Passo 1: Seja \( x \) e \( y \) as medidas dos segmentos \( AB \) e \( CD \):
- \( x + y = 12 \)
- \( x – y = 2 \)
Somando as equações:
\( (x + y) + (x – y) = 12 + 2 \Rightarrow 2x = 14 \Rightarrow x = 7 \)
Substituindo em \( x + y = 12 \):
\( 7 + y = 12 \Rightarrow y = 5 \)
Agora, para os segmentos \( EF \) e \( GH \):
Sabemos que o primeiro é o triplo do segundo menos duas unidades:
\( EF = 3 \cdot GH – 2 \)
Como os segmentos são proporcionais na mesma ordem:
\( AB : CD : EF : GH = 7 : 5 : (3g – 2) : g \)
Montamos a razão:
\( \frac{3g – 2}{g} = \frac{7}{5} \)
Multiplicando em cruz:
\( 5(3g – 2) = 7g \Rightarrow 15g – 10 = 7g \Rightarrow 8g = 10 \Rightarrow g = \frac{10}{8} = 1{,}25 \)
Agora:
- \( GH = g = 1{,}25 \)
- \( EF = 3g – 2 = 3 \cdot 1{,}25 – 2 = 3{,}75 – 2 = 1{,}75 \)
Somando tudo:
\( AB + CD + EF + GH = 7 + 5 + 1{,}75 + 1{,}25 = \boxed{15} \)
Resposta final: A soma das medidas dos quatro segmentos é 15.
🔗 Material complementar gratuito
Exercício 7
Clara precisa resolver o seguinte problema em sua aula de Matemática:
Na figura a seguir, as retas \( m, n \) e \( p \) são paralelas. Determine a medida do segmento \( \overline{FH} \).
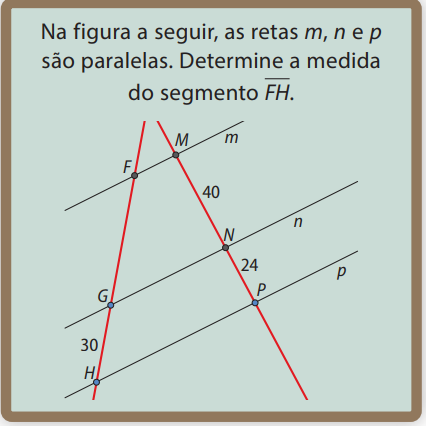
Para resolver o problema, Clara utilizou a proporção:
\( \frac{FH – 30}{30} = \frac{40}{24} \)
Reúna-se a um colega e respondam às questões:
- A proporção apresentada por Clara está correta? Justifiquem.
- Essa proporção resolve o problema? Justifiquem.
- Existe outra proporção que resolve o problema? Se sim, escrevam-na.
👇 Ver solução passo a passo
a) A proporção de Clara está correta?
Sim. Clara está comparando segmentos correspondentes das transversais que cruzam as retas paralelas:
- \( FH – 30 \) é o segmento \( FG \);
- \( GH = 30 \);
- \( MP = 40 \);
- \( PG = 24 \).
A proporção está montada entre segmentos correspondentes, portanto é válida.
b) Essa proporção resolve o problema?
Sim. Podemos resolver a equação a partir dela:
\( \frac{FH – 30}{30} = \frac{40}{24} \Rightarrow FH – 30 = \frac{40 \cdot 30}{24} = 50 \Rightarrow FH = 80 \)
c) Outra proporção possível:
\( \frac{FH}{30} = \frac{64}{24} \)
Aqui, Clara soma os segmentos da transversal da esquerda (\( FG + GH = FH \)) e compara com a soma dos segmentos da transversal da direita (\( MP + PG = 64 \)). A proporção continua válida.
Resposta final: \( FH = \boxed{80} \)
🔗 Material complementar gratuito
Exercício 8
A unidade de medida de temperatura usada no Brasil é o grau Celsius (°C). Em alguns países do mundo, como nos Estados Unidos, a unidade de medida padrão é o grau Fahrenheit (°F).
Para converter uma medida de temperatura de uma unidade para outra, usamos uma escala de correspondência, como indica a figura a seguir:
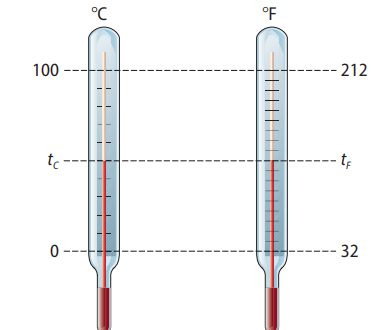
Agora, observe a fotografia:
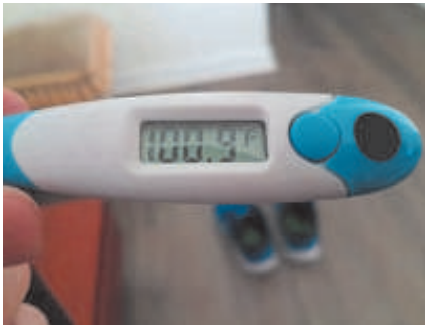
📍 O termômetro digital registra a temperatura em graus Fahrenheit.
Pergunta: Qual é a temperatura indicada na fotografia na escala Celsius?
👇 Ver solução passo a passo
Passo 1: Usar a fórmula de conversão de Fahrenheit para Celsius:
\( C = \frac{5}{9} \cdot (F – 32) \)
Passo 2: Substituir o valor indicado no visor do termômetro: \( F = 101{,}0 \)
\( C = \frac{5}{9} \cdot (101 – 32) = \frac{5}{9} \cdot 69 \)
Efetuando os cálculos:
\( C \approx \frac{5 \cdot 69}{9} = \frac{345}{9} \approx \boxed{38{,}28^\circ \text{C}} \)
Resposta final: A temperatura na escala Celsius é aproximadamente 38,28 °C.

























