Os polígonos são formas geométricas com lados retos e fechados, e entender a soma dos seus ângulos é essencial para resolver uma variedade de problemas de geometria. Neste artigo, exploraremos a soma dos ângulos internos e externos de um polígono e a relação entre eles.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
1. Soma dos Ângulos Internos de um Polígono
Definição: A soma dos ângulos internos de um polígono é a totalidade dos ângulos internos que formam a figura.
Fórmula Geral: Para encontrar a soma dos ângulos internos de um polígono, use a fórmula:

onde nnn é o número de lados do polígono.
Explicação:
- A fórmula é derivada da divisão do polígono em triângulos. Um polígono pode ser dividido em n−2 triângulos, e a soma dos ângulos internos de cada triângulo é 180 graus.
- Portanto, multiplicando o número de triângulos por 180 graus, obtemos a soma total dos ângulos internos.
Exemplo: Para um hexágono (um polígono com 6 lados):Soma dos ângulos internos=(6−2)×180°=4×180°=720°
Conclusão: A soma dos ângulos internos de um hexágono é 720 graus.
2. Soma dos Ângulos Externos de um Polígono
Definição: A soma dos ângulos externos de qualquer polígono, independentemente do número de lados, sempre é 360 graus.
Explicação:
- Os ângulos externos são formados entre um lado do polígono e a extensão do lado adjacente.
- A soma dos ângulos externos é sempre constante porque, ao dar uma volta completa ao redor do polígono, a soma dos ângulos externos é sempre uma volta completa, que equivale a 360 graus.
Fórmula Geral:
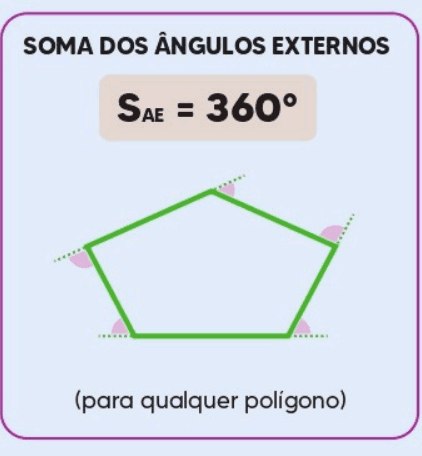
Exemplo: Para qualquer polígono, como um pentágono, a soma dos ângulos externos será sempre 360 graus, independentemente do número de lados.
Conclusão: A soma dos ângulos externos de um polígono é sempre 360 graus.
3. Relação entre Ângulo Interno e Ângulo Externo
Definição: Cada ângulo interno de um polígono e o ângulo externo correspondente são suplementares, ou seja, sua soma é sempre 180 graus.
Fórmula: Se Ai é ângulo interno e Ae é o ângulo externo correspondente:

Explicação:
- Um ângulo interno e o ângulo externo adjacente formam uma linha reta. Portanto, eles somam 180 graus.
- Isso é útil para calcular um dos ângulos se o outro é conhecido.
Exemplo: Para um quadrado (um polígono com 4 lados), cada ângulo interno mede 90 graus. O ângulo externo correspondente será:
Ângulo externo=180°−90°=90°
Conclusão: Para qualquer polígono, a soma de um ângulo interno e seu ângulo externo é sempre 180 graus.
A Soma dos Ângulos em Polígonos Regulares
Polígonos regulares são figuras geométricas com todos os lados e ângulos iguais. Conhecer a soma dos ângulos internos e externos desses polígonos é fundamental para resolver problemas de geometria e compreender melhor suas propriedades. Neste artigo, exploraremos a soma dos ângulos internos e externos de polígonos regulares e discutiremos alguns exemplos práticos.
1. Polígonos Regulares
Definição:
- Polígono Regular: Um polígono é considerado regular quando todos os seus lados e ângulos são iguais. Exemplos incluem o triângulo equilátero, o quadrado e o hexágono regular.
2. Soma dos Ângulos Internos de um Polígono Regular
Fórmula Geral: Para calcular a soma dos ângulos internos de um polígono regular, utilize a fórmula:

onde n é o número de lados do polígono.
Explicação:
- A fórmula é derivada da decomposição do polígono em triângulos. Cada polígono pode ser dividido em n−2 triângulos, e cada triângulo tem uma soma de ângulos internos de 180 graus.
- Multiplicando o número de triângulos por 180 graus, obtemos a soma total dos ângulos internos.
Exemplo: Para um octógono regular (um polígono com 8 lados):
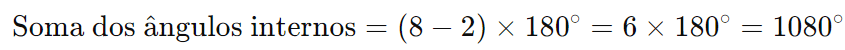
A soma dos ângulos internos de um octógono regular é 1080 graus.
3. Medida de Cada Ângulo Interno em um Polígono Regular
Fórmula Geral: Para encontrar a medida de cada ângulo interno de um polígono regular, use a fórmula:

onde n é o número de lados do polígono.
Explicação:
- Divida a soma total dos ângulos internos pelo número de lados para encontrar a medida de cada ângulo interno, pois todos os ângulos são iguais em um polígono regular.
Exemplo: Para um hexágono regular (um polígono com 6 lados):
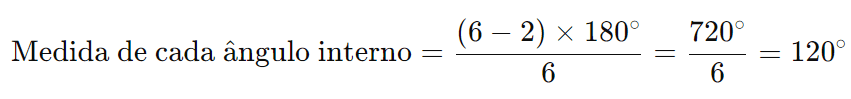
Conclusão: Cada ângulo interno de um hexágono regular mede 120 graus.
4. Soma dos Ângulos Externos de um Polígono Regular
Definição e Fórmula:
- Soma dos Ângulos Externos: A soma dos ângulos externos de qualquer polígono, regular ou irregular, é sempre 360 graus.
Explicação:
- Os ângulos externos são formados entre um lado do polígono e a extensão do lado adjacente.
- Ao percorrer toda a volta do polígono, a soma dos ângulos externos sempre corresponde a uma volta completa, que é 360 graus.
Conclusão: Para um polígono regular, assim como para qualquer polígono, a soma dos ângulos externos é 360 graus.
5. Medida de Cada Ângulo Externo em um Polígono Regular
Fórmula Geral: Para encontrar a medida de cada ângulo externo de um polígono regular, use a fórmula:
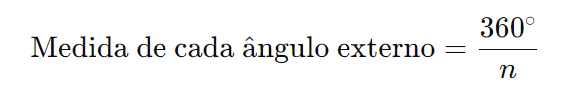
onde n é o número de lados do polígono.
Explicação:
- Divida a soma total dos ângulos externos (360 graus) pelo número de lados para encontrar a medida de cada ângulo externo, pois todos os ângulos são iguais em um polígono regular.
Exemplo: Para um octógono regular (um polígono com 8 lados):

Conclusão: Cada ângulo externo de um octógono regular mede 45 graus.
Regulares
Definição:
- Relação: Em um polígono regular, cada ângulo interno e seu ângulo externo adjacente somam 180 graus.
Fórmula: Se Ai é ângulo interno e Ae é o ângulo externo correspondente:
Ai + Ae = 180°
Conclusão: Essa relação é útil para verificar a precisão dos cálculos de ângulos internos e externos em polígonos regulares.
Conclusão
Entender a soma dos ângulos internos e externos de um polígono é essencial para muitas aplicações em geometria e design. A fórmula para a soma dos ângulos internos permite calcular rapidamente a soma total de ângulos em qualquer polígono, enquanto a constância da soma dos ângulos externos ajuda na análise das propriedades geométricas das formas. A relação entre ângulos internos e externos também é uma ferramenta valiosa para resolver problemas geométricos. Com essas informações, é possível abordar e resolver uma ampla gama de questões relacionadas a polígonos.
Entender a soma dos ângulos internos e externos de polígonos regulares é crucial para a resolução de problemas geométricos e para a compreensão das propriedades desses polígonos. Com as fórmulas e conceitos apresentados, é possível calcular rapidamente a soma dos ângulos e a medida de cada ângulo interno e externo, aplicando esses conhecimentos em diversas situações práticas e teóricas.
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes