Alturas
A altura de um triângulo é o segmento de reta que parte de um vértice e forma um ângulo reto (90°) com o lado oposto, ou com a sua extensão, no caso de triângulos obtusângulos. Cada triângulo possui três alturas, uma para cada vértice. As alturas representam a distância perpendicular entre um vértice e o lado oposto.
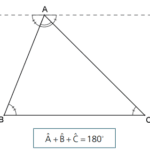
Num triângulo ABC, tracemos pelo ponto A uma reta r perpendicular à reta que contém o lado BC.
A reta que contém o lado BC, reta BC, é chamada de reta suporte do lado BC.
Chamemos de H1 o ponto de encontro da reta r com a reta BC:
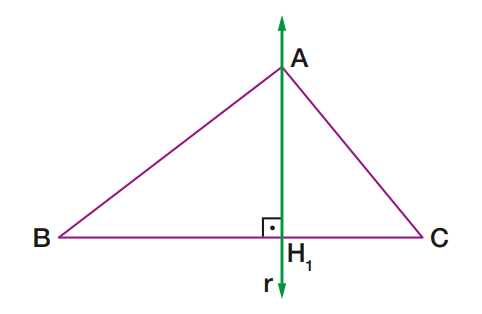
Destaquemos o segmento AH1 :
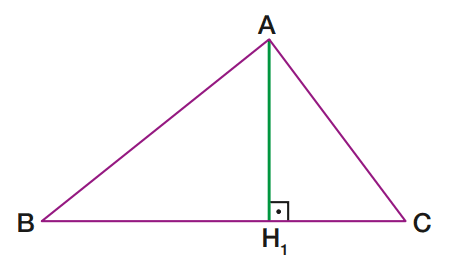
O segmento AH1 é uma altura do triângulo ABC.
O ponto H1 é a interseção da reta BC com a perpendicular a ela conduzida pelo ponto A. H1
também é chamado pé da altura.
Altura de um triângulo é o segmento perpendicular à reta suporte de um lado, com extremidade nessa reta e no vértice oposto a esse lado.
Ortocentro
O ortocentro é o ponto de encontro das três alturas de um triângulo. A posição do ortocentro depende do tipo de triângulo:
- Em um triângulo acutângulo (todos os ângulos menores que 90°), o ortocentro está dentro do triângulo.
- Em um triângulo retângulo, o ortocentro coincide com o vértice do ângulo reto.
- Em um triângulo obtusângulo (um ângulo maior que 90°), o ortocentro está localizado fora do triângulo.
O ortocentro é um ponto notável, pois, apesar de não ser tão fácil de visualizar como o baricentro ou incentro, ele desempenha um papel importante em várias propriedades geométricas e teoremas envolvendo triângulos.
Um triângulo tem três alturas. Observe:
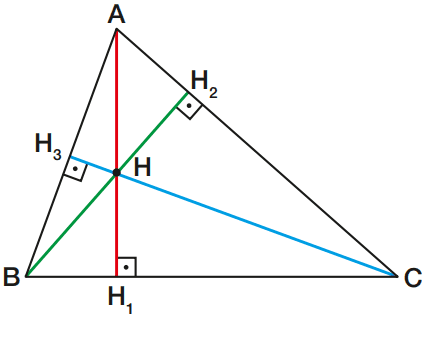
Nas figuras acima, as três alturas são:
- AH1, altura relativa ao lado BC ou ao vértice A;
- BH2 altura relativa ao lado AC ou ao vértice B;
- CH3, altura relativa ao lado AB ou ao vértice C.
As três alturas, ou os seus prolongamentos, encontram-se num ponto chamado ortocentro do triângulo.
Nas figuras acima, H é o ortocentro do triângulo ABC, o qual pode ser interno ao triângulo (quando o triângulo ABC é acutângulo) ou externo ao triângulo (quando o triângulo ABC é obtusângulo).
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Leia também…
Pontos Notáveis do Triângulo e Propriedades
Lista de exercício com solução de Pontos Notáveis do Triângulo