As razões trigonométricas dos ângulos notáveis — 30º, 45º e 60º — são fundamentais para a resolução de problemas envolvendo triângulos. Conhecê-las de forma exata evita a necessidade de cálculos aproximados com uso de calculadora, tornando a resolução mais rápida e prática.
Por que 30º, 45º e 60º são ângulos notáveis?
Esses ângulos recebem destaque porque suas razões trigonométricas (seno, cosseno e tangente) podem ser determinadas a partir de construções geométricas simples:
- O triângulo equilátero, ao ser dividido ao meio, gera ângulos de 30º e 60º.
- O triângulo retângulo isósceles, com catetos iguais, forma ângulos de 45º.
A partir dessas figuras, encontramos valores exatos para as funções trigonométricas, sem depender de aproximações decimais.
Seno, Cosseno e Tangente de 30º e 60º
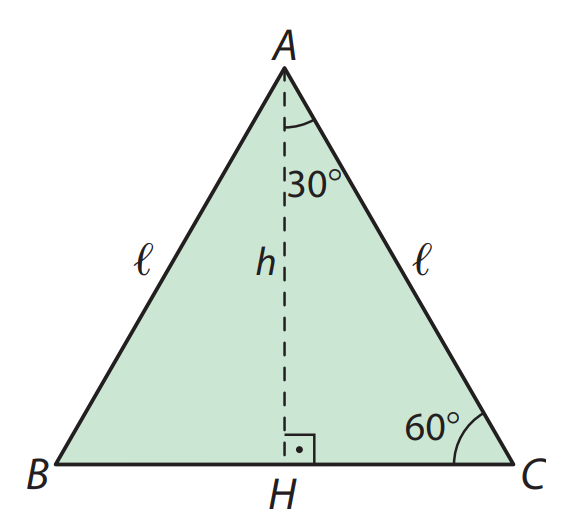
Considere um triângulo equilátero de lado \( \ell \). Ao traçarmos a altura, dividimos o triângulo em dois triângulos retângulos, cada um com ângulos de 30º e 60º.
Pelo Teorema de Pitágoras, a altura \( h \) será:
Assim, no triângulo retângulo formado, temos:
- \( \sin 30º = \frac{\ell/2}{\ell} = \frac{1}{2} \)
- \( \cos 30º = \frac{h}{\ell} = \frac{\sqrt{3}}{2} \)
- \( \tan 30º = \frac{\ell/2}{h} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3} \)
- \( \sin 60º = \frac{h}{\ell} = \frac{\sqrt{3}}{2} \)
- \( \cos 60º = \frac{\ell/2}{\ell} = \frac{1}{2} \)
- \( \tan 60º = \frac{h}{\ell/2} = \sqrt{3} \)
Seno, Cosseno e Tangente de 45º
Para os ângulos de 45º, considere um triângulo retângulo isósceles com catetos iguais (\( \ell \)). A hipotenusa pode ser calculada pelo Teorema de Pitágoras:
Assim, temos:
- \( \sin 45º = \frac{\ell}{\ell \sqrt{2}} = \frac{\sqrt{2}}{2} \)
- \( \cos 45º = \frac{\ell}{\ell \sqrt{2}} = \frac{\sqrt{2}}{2} \)
- \( \tan 45º = \frac{\ell}{\ell} = 1 \)
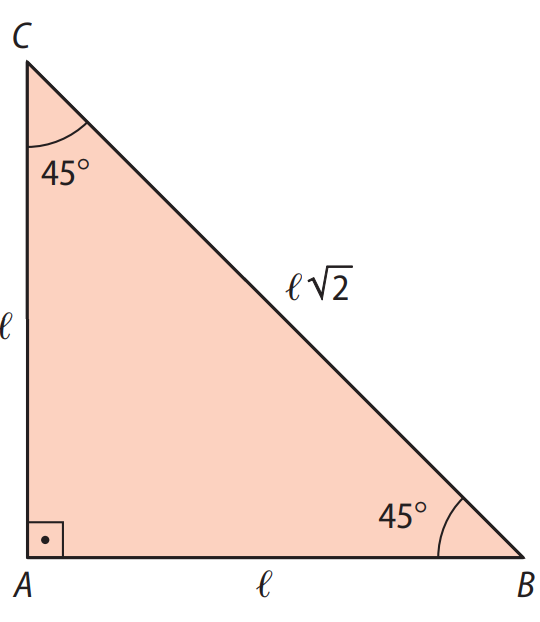
Tabela Resumida dos Valores
A tabela abaixo organiza os valores de forma prática:
| Ângulo | \( \sin \) | \( \cos \) | \( \tan \) |
|---|---|---|---|
| 30º | \( \frac{1}{2} \) | \( \frac{\sqrt{3}}{2} \) | \( \frac{\sqrt{3}}{3} \) |
| 45º | \( \frac{\sqrt{2}}{2} \) | \( \frac{\sqrt{2}}{2} \) | 1 |
| 60º | \( \frac{\sqrt{3}}{2} \) | \( \frac{1}{2} \) | \( \sqrt{3} \) |
Como utilizar essas razões?
Essas razões trigonométricas são amplamente utilizadas em:
- Cálculo de lados de triângulos: Conhecendo um lado e um ângulo, encontramos os demais lados usando seno, cosseno ou tangente.
- Problemas de altura e distância: Situações reais como medir prédios e torres.
- Provas e concursos: Muitos exercícios exigem que se conheçam esses valores de forma exata.
Exemplos práticos
Exemplo 1:
Calcule o valor do cateto oposto em um triângulo retângulo onde a hipotenusa mede 10 e o ângulo é 30º.
Solução:
Exemplo 2:
Determine a altura de um triângulo equilátero com lado \( \ell = 8 \).
Solução:
Exercício Resolvido – UFV-MG
Enunciado:
Um navio, navegando em linha reta, passa sucessivamente pelos pontos A, B e C.
O comandante, quando o navio está em A, observa um farol F e determina que o ângulo \( \widehat{FÂC} \) mede \(30^\circ\).
Após navegar 6 km até o ponto B, ele verifica que o ângulo \( \widehat{FBC} \) mede \(90^\circ\).
Calcule a distância, em km, que separa o farol F do navio quando este se encontra no ponto C, situado a 2 km do ponto B.
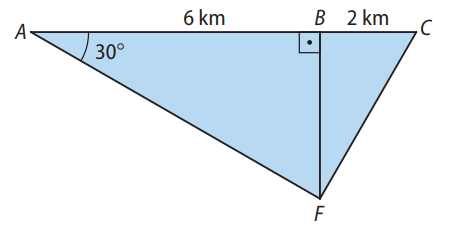
Resolução:
Do triângulo retângulo \( ABF \), temos:
Logo, a distância \( BF \) é igual a \( 2 \sqrt{3} \, \text{km} \).
Aplicando o Teorema de Pitágoras no triângulo \( BCF \):
\( (CF)^2 = (2 \sqrt{3})^2 + 2^2 \)
\( CF = \sqrt{16} \)
\( CF = 4 \, \text{km} \).
Portanto, a distância entre o farol F e o navio no ponto C é de 4 km.
Exercício Resolvido – Largura do Rio
Enunciado:
Suponha que um rio apresente um trecho de margens retas e paralelas, conforme a figura.
Os pontos A e B pertencem a uma das margens e C pertence à outra. Sabendo que
\( \widehat{A\hat{B}C} = 60^\circ \), \( \widehat{B\hat{A}C} = 90^\circ \) e \( AB = 25 \, \text{m} \),
calcule a largura \( AC \) do rio.
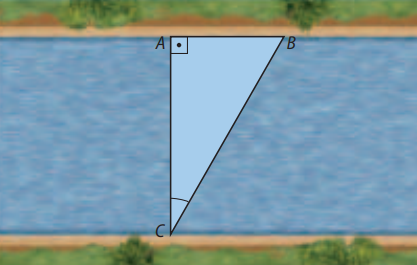
Resolução:
Considere o triângulo \( ABC \), sendo \( AC = x \).
Portanto, a largura do rio é de 25\( \sqrt{3} \, \text{m} \).
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon📚 Livros que Você Precisa Ter em Sua Biblioteca
O Livro da Matemática
Uma obra essencial para entender os principais conceitos matemáticos de forma clara e prática.
🔗 Acesse na AmazonO Grande Livro de Matemática do Manual do Mundo
Um guia incrível criado pelo Manual do Mundo para aprender matemática de forma divertida e eficiente.
🔗 Acesse na AmazonSou Péssimo em Matemática
Livro perfeito para quem quer superar bloqueios com a matemática e aprender de forma leve e prática.
🔗 Acesse na Amazon