A circunferência é uma figura geométrica fascinante, rica em propriedades que formam a base de muitos conceitos em geometria. Entre essas propriedades, os ângulos associados à circunferência desempenham um papel fundamental. Neste artigo, vamos explorar quatro tipos principais de ângulos: ângulo central, ângulo inscrito, ângulo excêntrico interior e ângulo excêntrico exterior.
Ângulo Central
O ângulo central é formado por dois raios que partem do centro da circunferência e interceptam um arco. Uma característica importante desse tipo de ângulo é que sua medida é igual à medida do arco correspondente.
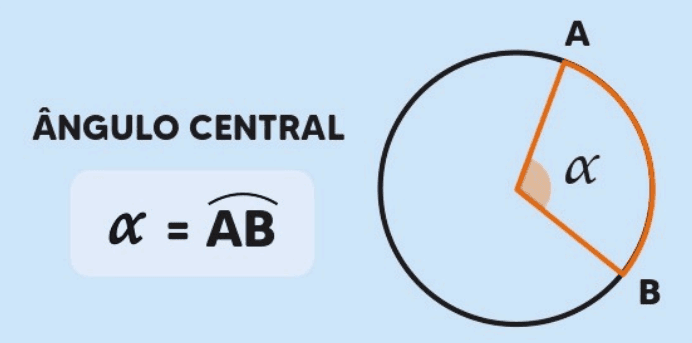
Por exemplo, se um arco AB na circunferência mede 60°, o ângulo central ∠AOB, formado pelos raios OA e OB, também mede 60°.
Este tipo de ângulo é fundamental para o cálculo de arcos, setores circulares e até mesmo em problemas envolvendo trigonometria. A simplicidade de sua relação direta com o arco torna o ângulo central um dos conceitos mais básicos e utilizados em geometria.
Ângulo Inscrito
O ângulo inscrito é formado por dois pontos na circunferência que, ao serem unidos por uma corda, formam um vértice na própria circunferência. Ao contrário do ângulo central, a medida do ângulo inscrito é sempre metade da medida do arco correspondente.
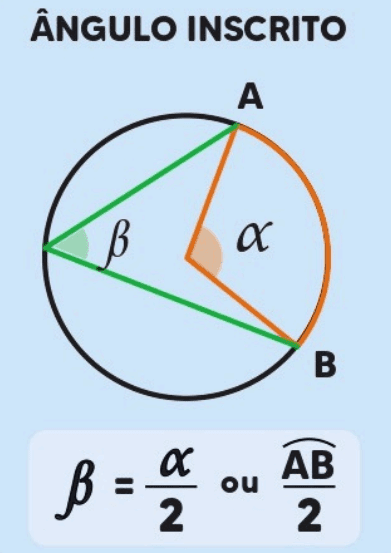
Assim, se o arco AB mede 80°, o ângulo inscrito ∠ACB, onde o ponto C está na circunferência, mede 40°.
Esse tipo de ângulo tem várias aplicações, especialmente na resolução de problemas envolvendo quadriláteros cíclicos (quadriláteros cujos vértices estão sobre a circunferência). Além disso, ele é usado para provar teoremas importantes, como o Teorema do Ângulo Inscrito, que afirma que todos os ângulos inscritos em um mesmo arco são iguais.
Ângulo Excêntrico Interior
O ângulo excêntrico interior é formado por dois segmentos de reta que interceptam a circunferência em pontos distintos, mas cujo vértice não está na circunferência e sim no interior dela. Esse ângulo é interessante porque sua medida é dada pela semissoma dos arcos interceptados. Especificamente, se AB e CD são as cordas que formam o ângulo, então a medida do ângulo excêntrico interior é dada por:
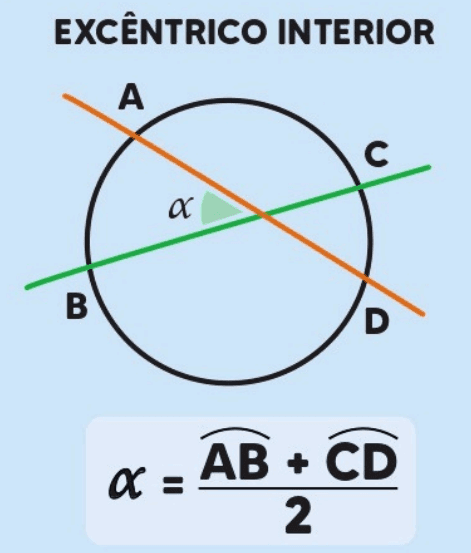
Este conceito é útil em problemas envolvendo interseções de cordas e também em situações em que se deseja calcular ângulos em figuras complexas.
Exemplo: Calcule o valor do ângulo α na circunferência sabendo que C não é o centro da circunferência.
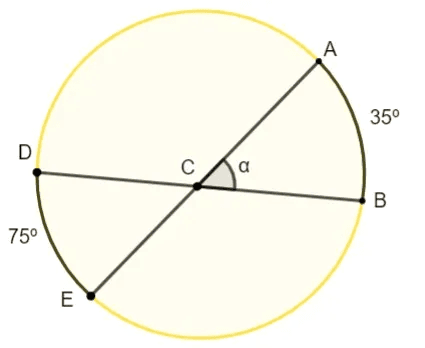
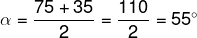
Ângulo Excêntrico Exterior
O ângulo excêntrico exterior é formado por duas secantes, uma secante e uma tangente, ou duas tangentes que se interceptam fora da circunferência. A medida desse ângulo é dada pela diferença entre os arcos interceptados pelas secantes ou tangentes. Se AB e CD são os arcos interceptados pelas secantes, a medida do ângulo excêntrico exterior é:
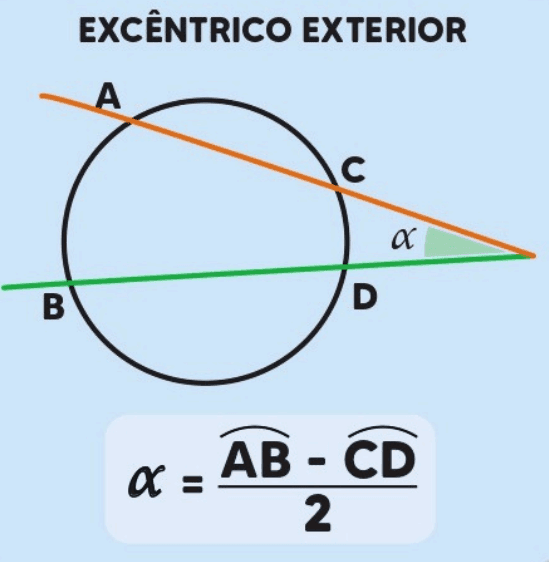
Esse tipo de ângulo é muito útil em problemas que envolvem tangentes e secantes, especialmente em situações que requerem a determinação de ângulos externos à circunferência.
Exemplo: Calcule o valor do ângulo α.
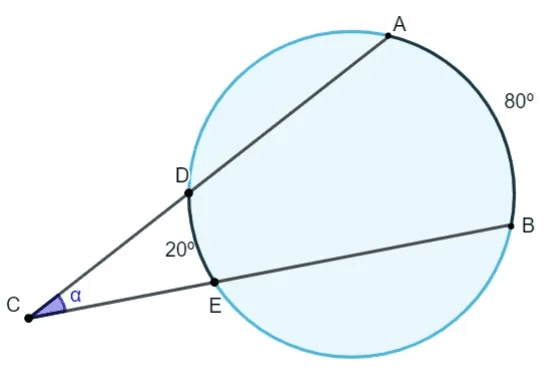
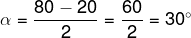
Conclusão
Compreender os diferentes tipos de ângulos na circunferência é crucial para dominar a geometria plana e suas aplicações. O ângulo central, com sua relação direta com o arco, o ângulo inscrito, com sua propriedade de ser metade do arco correspondente, e os ângulos excêntricos, interior e exterior, com suas fórmulas específicas, fornecem uma base sólida para resolver uma ampla gama de problemas geométricos. Esses conceitos não só aprimoram a compreensão matemática, mas também abrem portas para aplicações em áreas como física, engenharia e outras disciplinas que dependem da geometria.
Esses ângulos são mais do que meras medidas; eles são ferramentas poderosas para explorar as propriedades das circunferências e dos polígonos associados a elas, permitindo que matemáticos e estudantes desvendem a beleza da geometria em suas formas mais puras.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes
Ângulos na Circunferência: Uma Exploração Completa













