Área de Figuras Planas: Como Calcular, Exercícios Resolvidos

A geometria é uma parte essencial da matemática que se conecta diretamente com o mundo ao nosso redor. Uma das suas aplicações mais comuns é o cálculo da área de figuras planas, que são formas bidimensionais limitadas por linhas retas ou curvas. Entender como calcular a área dessas figuras é fundamental em diversas situações cotidianas, desde a decoração de um ambiente até a construção civil. Neste artigo, exploraremos como determinar a área de cinco figuras planas muito comuns: quadrado, retângulo, trapézio, losango e paralelogramo.

1. Quadrado

Definição: O quadrado é uma figura plana com quatro lados iguais e quatro ângulos retos (90°).

Fórmula para a Área:
Área = Lado²

Explicação: Como todos os lados de um quadrado são iguais, basta multiplicar a medida de um dos lados por si mesma para encontrar a área.

Exemplo: Se o lado de um quadrado é 5 cm, a área será:
Área = 5² = 25cm²

Aplicação Prática: Suponha que você queira comprar um tapete quadrado para sua sala. Sabendo que a sala tem um lado de 4 metros, a área do tapete necessário seria:
Área = 4² = 16 m²

2. Retângulo

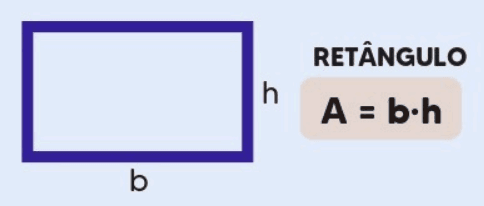
Definição: O retângulo é uma figura plana com quatro lados, onde os lados opostos são iguais e todos os ângulos são retos (90°).

Fórmula para a Área:
Área = Basex x Altura

Explicação: A área de um retângulo é calculada multiplicando a base pela altura, que correspondem aos lados adjacentes da figura.

Exemplo: Se um retângulo tem uma base de 8 cm e altura de 3 cm, a área será:
Área = 8 x 3 = 24 cm²

Aplicação Prática: Imagine que você quer pintar uma parede retangular de 6 metros de comprimento e 2,5 metros de altura. A área a ser pintada será:
Área = 6 x 2,5 = 15m²

3. Trapézio

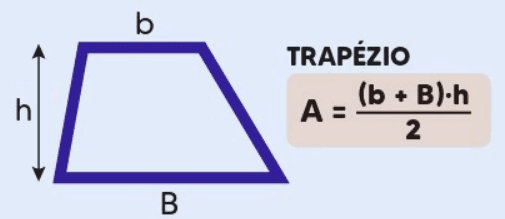
Definição: O trapézio é uma figura plana com quatro lados, sendo dois deles paralelos, chamados de bases. As outras duas arestas podem ser de tamanhos diferentes.

Fórmula para a Área:
Área = [(Base Maior + Base Menor)xAltura]/2

Explicação: A área do trapézio é encontrada somando as medidas das bases, multiplicando pela altura (a distância entre as bases) e dividindo o resultado por dois.

Exemplo: Se um trapézio tem uma base maior de 10 cm, uma base menor de 6 cm e uma altura de 4 cm, a área será:
Área[(10 + 6) x 4]/2 = 16 x 4 / 2 = 32 cm²

Aplicação Prática: Suponha que você tenha um terreno em formato de trapézio e deseja cobri-lo com grama. Se as bases são de 12 metros e 8 metros, e a altura é de 5 metros, a área a ser coberta será:
Área = [(12 + 8)x 5/]2 = 20 x 5/2 = 50 m²

4. Losango

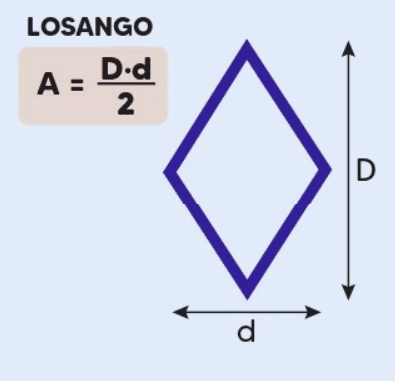
Definição: O losango é uma figura plana com quatro lados iguais e ângulos opostos iguais, que podem ser diferentes de 90°.

Fórmula para a Área:
Área = (Diagonal Maior x Diagonal Menor) /2

Explicação: A área do losango é obtida multiplicando as diagonais (as linhas que ligam os vértices opostos) e dividindo o resultado por dois.

Exemplo: Se um losango tem uma diagonal maior de 10 cm e uma diagonal menor de 6 cm, a área será:
Área = (10 x 6)/2 = 30cm²

Aplicação Prática: Imagine que você possui um terreno em forma de losango com diagonais de 14 metros e 8 metros. A área do terreno será:
Área = (14 x 8) / 2 = 56m²

5. Paralelogramo

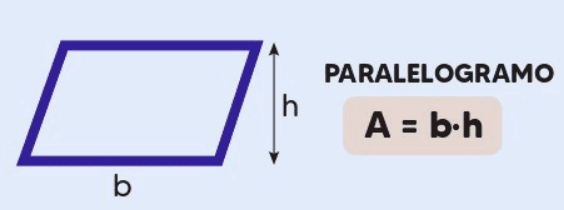
Definição: O paralelogramo é uma figura plana com dois pares de lados paralelos e opostos de medidas iguais.

Fórmula para a Área:
Área = Base x Altura

Explicação: Assim como no retângulo, a área do paralelogramo é dada pela multiplicação da base pela altura, mas a altura deve ser perpendicular à base.

Exemplo: Se um paralelogramo tem uma base de 7 cm e uma altura de 4 cm, a área será:
Área = 7 x 4 = 28cm²

Aplicação Prática: Suponha que você queira instalar um painel solar em um telhado que tem a forma de um paralelogramo com uma base de 10 metros e altura de 6 metros. A área disponível para os painéis será:
Área = 10 6 = 60m²

Exercícios Resolvidos de Áreas de Figuras Planas

Aqui estão dois exercícios resolvidos para cada tipo de figura plana abordada no artigo:

1. Quadrado

Exercício 1:
Um terreno quadrado tem 15 metros de lado. Qual é a área do terreno?

Resolução:
Área = Lado²
Área} = 15² = 225m²
Resposta: A área do terreno é de 225 m².

Exercício 2:
Um quadrado possui uma área de 64 cm². Qual é o comprimento do lado desse quadrado?

Resolução:
Área} = Lado²
64 = Lado²
Lado = √64 = 8 cm
Resposta: O lado do quadrado é de 8 cm.

2. Retângulo

Exercício 1:
Uma sala retangular tem 7 metros de comprimento e 4 metros de largura. Qual é a área da sala?

Resolução:
Área= Base x Altura
Área = 7 x 4 = 28m²
Resposta: A área da sala é de 28 m².

Exercício 2:
Um campo de futebol tem a forma de um retângulo com 90 metros de comprimento e 60 metros de largura. Qual é a área do campo?

Resolução:
Área = Base x Altura
Área} = 90 x 60 = 5400m²
Resposta: A área do campo de futebol é de 5400 m².

3. Trapézio

Exercício 1:
Um trapézio tem bases de 12 cm e 8 cm, e a altura é de 5 cm. Qual é a área do trapézio?

Resolução:
Área = [ (Base Maior + Base Menor) x Altura] /2
Área} = [(12 + 8) x 5]/2 = 50cm²
Resposta: A área do trapézio é de 50 cm².

Exercício 2:
As bases de um trapézio medem 18 cm e 10 cm, e a altura é de 6 cm. Calcule a área desse trapézio.

Resolução:
Área = [ (Base Maior + Base Menor) x Altura] /2

Área} = [(18 + 10) x 6]/2 = 28 x 6 / 2 = 84 cm²
Resposta: A área do trapézio é de 84 cm².

4. Losango

Exercício 1:
Um losango tem as diagonais medindo 16 cm e 10 cm. Qual é a área do losango?

Resolução:
Área = (Diagonal Maior x Diagonal Menor) /2

Área} = (16 x 10)/2 = 160/2 = 80cm²
Resposta: A área do losango é de 80 cm².

Exercício 2:
As diagonais de um losango medem 24 cm e 18 cm. Calcule a área desse losango.

Resolução:
Área = (Diagonal Maior x Diagonal Menor) /2

Área} = (24 x 18)/2 = 432/2 = 216cm²
Resposta: A área do losango é de 216 cm².

5. Paralelogramo

Exercício 1:
Um paralelogramo tem uma base de 9 cm e uma altura de 5 cm. Qual é a área do paralelogramo?

Resolução:
Área = Base x Altura
Área} = 9 x 5 = 45cm²
Resposta: A área do paralelogramo é de 45 cm².

Exercício 2:
As dimensões de um paralelogramo são base de 12 metros e altura de 7 metros. Calcule a área desse paralelogramo.

Resolução:
Área = Base x Altura
Área = 12 x7 = 84 m²
Resposta: A área do paralelogramo é de 84 m².

Conclusão

Compreender o cálculo da área das figuras planas é crucial para diversas atividades do dia a dia, desde projetos de design e arquitetura até tarefas simples como escolher um novo piso ou mobiliar um espaço. O domínio dessas fórmulas matemáticas básicas não só ajuda na resolução de problemas práticos como também desenvolve o raciocínio lógico e a habilidade de estimar espaços e proporções. Com este guia, você tem agora as ferramentas para calcular a área de quadrados, retângulos, trapézios, losangos e paralelogramos, aplicando esses conhecimentos de forma eficaz em suas tarefas cotidianas.

Leia também

Área de Triângulos: Conceitos e Cálculos

Área de Figuras Planas: Como Calcular, Exercícios Resolvidos

Área de Circunferências: Explorando Formas e Cálculos

Explorando Ângulos: Agudo, Obtuso, Reto e Raso

Retas Paralelas e Transversais

A Soma dos Ângulos em Polígonos: Internos e Externos

Tudo Sobre Triângulos: Classificação e Propriedades 

Congruência de Triângulos: Casos e Propriedades 

Teorema de Pitágoras: Conceito, Provas e Aplicações 

Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais

A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria 

Quadriláteros: Área, Perímetro e Diagonais 

Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos 

Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares

Quadriláteros Circunscritos: Teorema de Pitot

Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes 

Ângulos na Circunferência: Uma Exploração Completa