Os arranjos são um dos pilares da análise combinatória, usados para resolver problemas que envolvem a seleção e a organização de elementos. Diferentemente de outros conceitos, como combinações, os arranjos levam em conta a ordem dos itens escolhidos, o que pode gerar resultados totalmente diferentes dependendo da disposição.
Este artigo é um guia completo para entender o conceito de arranjo, com explicações claras e exemplos práticos. Vamos abordar os dois tipos principais de arranjo: simples e com repetição.

📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade

Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!
O Que É um Arranjo?
Um arranjo é uma forma de organizar ou selecionar elementos de um conjunto, considerando que a ordem dos itens importa. Isso significa que trocar a posição dos elementos gera uma nova disposição, e cada uma dessas disposições é contada separadamente.
Por exemplo:
- Se temos as letras A, B e C e escolhemos duas, as disposições possíveis são AB, BA, AC, CA, BC e CB. Note que AB é diferente de BA, pois a ordem importa.
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
Tipos de Arranjos
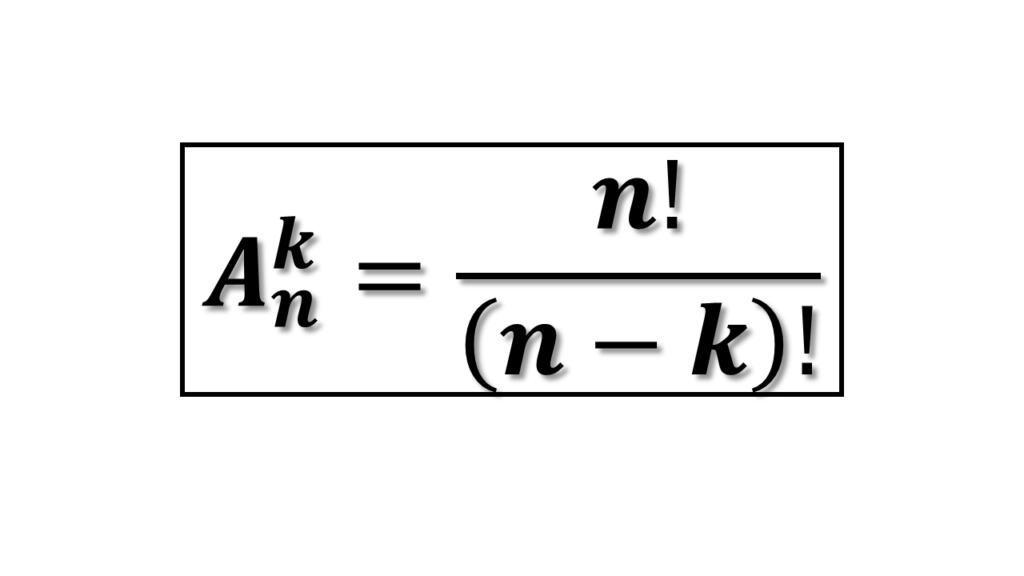
1. Arranjo Simples
O arranjo simples ocorre quando escolhemos e organizamos uma parte (k) dos elementos de um conjunto (n), sem permitir repetições.
Fórmula do Arranjo Simples:
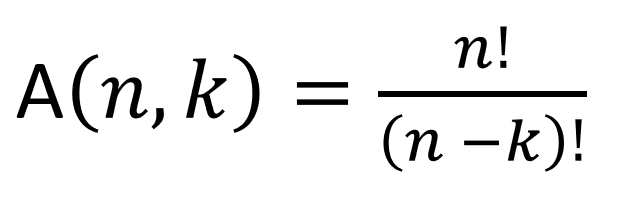
- n: número total de elementos no conjunto.
- k: número de elementos escolhidos para o arranjo.
- ! (fatorial): produto de todos os números inteiros positivos até o número indicado.
Exemplo Prático:
Imagine que você tem 5 candidatos para ocupar 2 cargos em uma empresa (presidente e vice-presidente). Quantas disposições diferentes podem ser feitas?
Solução:
- Total de candidatos (n): 5.
- Cargos a serem preenchidos (k): 2.
Cálculo:
A(5,2) = 5!/(5−2)! = (5×4×3!)/3! = 5×4 = 20
Há 20 formas diferentes de organizar os candidatos.
2. Arranjo com Repetição
O arranjo com repetição é usado quando os elementos do conjunto podem ser repetidos. Nesse caso, cada elemento pode aparecer mais de uma vez nas combinações.
Fórmula do Arranjo com Repetição:
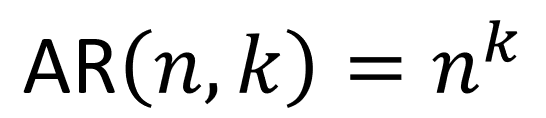
- n: número total de elementos no conjunto.
- k: número de elementos escolhidos para o arranjo, permitindo repetições.
Exemplo Prático:
Você deseja criar uma senha de 3 caracteres usando as letras A, B e C, podendo repetir letras. Quantas combinações diferentes podem ser formadas?
Solução:
- Total de letras (n): 3.
- Número de caracteres da senha (k): 3.
Cálculo:
AR(3,3) = 33 = 27
Portanto, é possível criar 27 senhas diferentes.
“Quer dominar os cálculos de possibilidades e resolver problemas de contagem com facilidade? Confira nosso artigo completo sobre as Fórmulas da Análise Combinatória e aprenda como aplicá-las no seu dia a dia com exemplos claros e objetivos!
Diferença Entre Arranjo Simples e Arranjo com Repetição
| Característica | Arranjo Simples | Arranjo com Repetição |
|---|---|---|
| Repetição de Elementos | Não é permitida | É permitida |
| Fórmula | 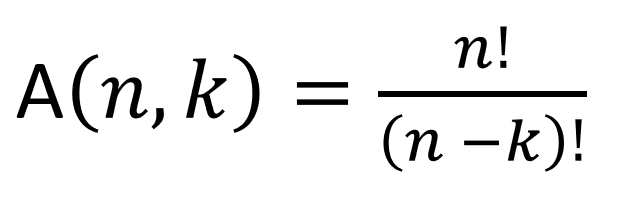 | 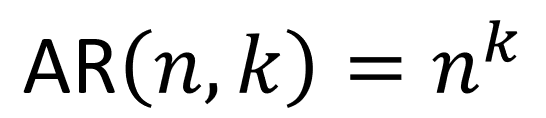 |
| Exemplo Prático | Organizar 3 pessoas em 2 posições | Criar senhas com repetição de letras |
Aplicações dos Arranjos
Os arranjos aparecem em diversas situações práticas, como:
- Planejamento e Organização:
Determinar a ordem de apresentação de palestrantes ou a disposição de mesas em eventos. - Segurança Digital:
Calcular o número de combinações possíveis de senhas ou códigos, com ou sem repetição de caracteres. - Logística:
Planejar a ordem de entrega de encomendas em diferentes rotas. - Esportes:
Organizar a posição de atletas em competições, onde a ordem de chegada importa.
Resumo Prático
- Use arranjo simples quando a ordem importa e não há repetição de elementos.
- Use arranjo com repetição quando a ordem importa e os elementos podem se repetir.
- Identifique o tipo de problema e aplique a fórmula adequada para encontrar o número total de possibilidades.
Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!
Conclusão
Os arranjos são uma parte essencial da análise combinatória dentro da matemática, assim como a permutação e a combinação, usados para resolver problemas onde a ordem faz diferença. Seja na criação de senhas, organização de eventos ou planejamento de tarefas, eles ajudam a calcular possibilidades de forma clara e eficiente.
Compreender a diferença entre arranjo simples e com repetição permite aplicar o conceito corretamente em diferentes contextos, tornando-o uma ferramenta indispensável para resolver problemas práticos e acadêmicos.
























