Bissetrizes e incentro

Bissetrizes

Uma bissetriz de um triângulo é um segmento de reta que divide um ângulo interno em duas partes iguais. Em um triângulo, existem três bissetrizes, uma para cada ângulo. Elas têm a propriedade de serem equidistantes dos dois lados do ângulo que estão dividindo.

Num triângulo ABC, tracemos a bissetriz AS₁, relativa ao ângulo A. Chamemos de S₁ o ponto de encontro da bissetriz com o lado BC.

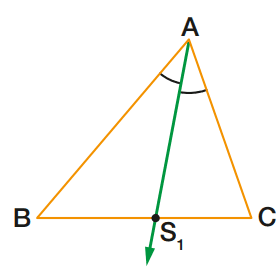
Destaquemos o segmento AS₁.

O segmento AS₁ é uma bissetriz do triângulo ABC.

Observe que:

• o segmento AS₁ está contido na semirreta AS₁ (bissetriz do ângulo A);

• S₁ é a interseção do lado BC com a bissetriz do ângulo A

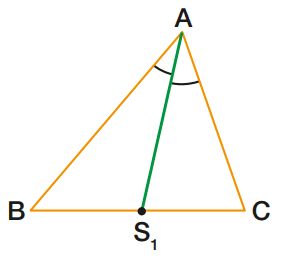
Bissetriz de um triângulo é um segmento com extremidades num vértice e no lado oposto e que divide o ângulo desse vértice em dois ângulos congruentes.

Incentro

O incentro é o ponto de encontro das três bissetrizes de um triângulo. Esse ponto é o centro do círculo inscrito no triângulo, ou seja, o círculo que toca todos os três lados do triângulo internamente. O incentro é equidistante dos três lados do triângulo, o que significa que a distância do incentro até qualquer um dos lados do triângulo é a mesma.

Assim como o baricentro, o incentro está sempre dentro do triângulo, independentemente de sua forma (acutângulo, retângulo ou obtusângulo).

Um triângulo tem três bissetrizes. Na figura, as três bissetrizes são:

• AS₁, bissetriz relativa ao lado BC ou ao vértice A;
• BS₂, bissetriz relativa ao lado AC ou ao vértice B;
• CS₃, bissetriz relativa ao lado AB ou ao vértice C.

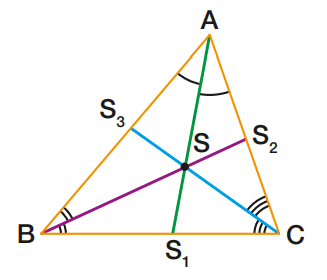
As três bissetrizes de um triângulo encontram-se num ponto chamado incentro do triângulo

Na figura acima, S é o incentro do triângulo ABC.

A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.

Leia também…

Pontos Notáveis do Triângulo e Propriedades

Lista de exercício com solução de Pontos Notáveis do Triângulo