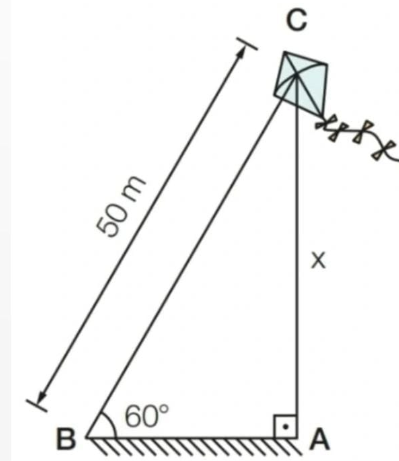
Uma pipa está presa a um fio de 50 metros que forma um ângulo de 60° com o chão. Qual a altura x da pipa em relação ao solo? Considere as alternativas:
A) 25√5
B) 40√2
C) 25√3
D) 43√5
Ver Solução
Vamos resolver uma questão de matemática aplicada à geometria plana, explorando conceitos fundamentais de trigonometria.
Entendendo o enunciado
O triângulo retângulo é formado por:
- Hipotenusa: BC=50 m
- Ângulo: ∠ABC=60°
- Altura da pipa: x, o cateto oposto ao ângulo de 60°
A pergunta é: qual o valor da altura xx?
Resolução passo a passo
Razão trigonométrica: Utilizaremos a relação:
sin(60°) = cateto oposto/hipotenusa
Substituindo os valores:
sin(60°) = x/50
Valor de sin(60°): Sabemos que:
sin(60°) = (√3/2)
Assim, temos: √3/2 = x/50
Isolando x: Multiplicando ambos os lados por 50:
x = 50⋅(√3/2)x
Simplificando: x = 25√3
Identificando a resposta: Comparando o resultado com as alternativas, temos:
A altura x = 25√3, correspondendo à alternativa C).
Resposta final
A altura da pipa é: C) 25√3
Gostou dessa questão? Que tal desafiar ainda mais seus conhecimentos? Clique aqui e resolva outra questão matemática preparada especialmente para você! 📚✨
Mais questões de Geometria Plana
🟢Mapas Mentais de Matemática para Concurso
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
Pronto para mergulhar em mais desafios matemáticos? 🚀 Explore nossa categoria completa com diversas questões matemática para testar e aprimorar seus conhecimentos! Clique aqui e comece agora! 📘✔️”
