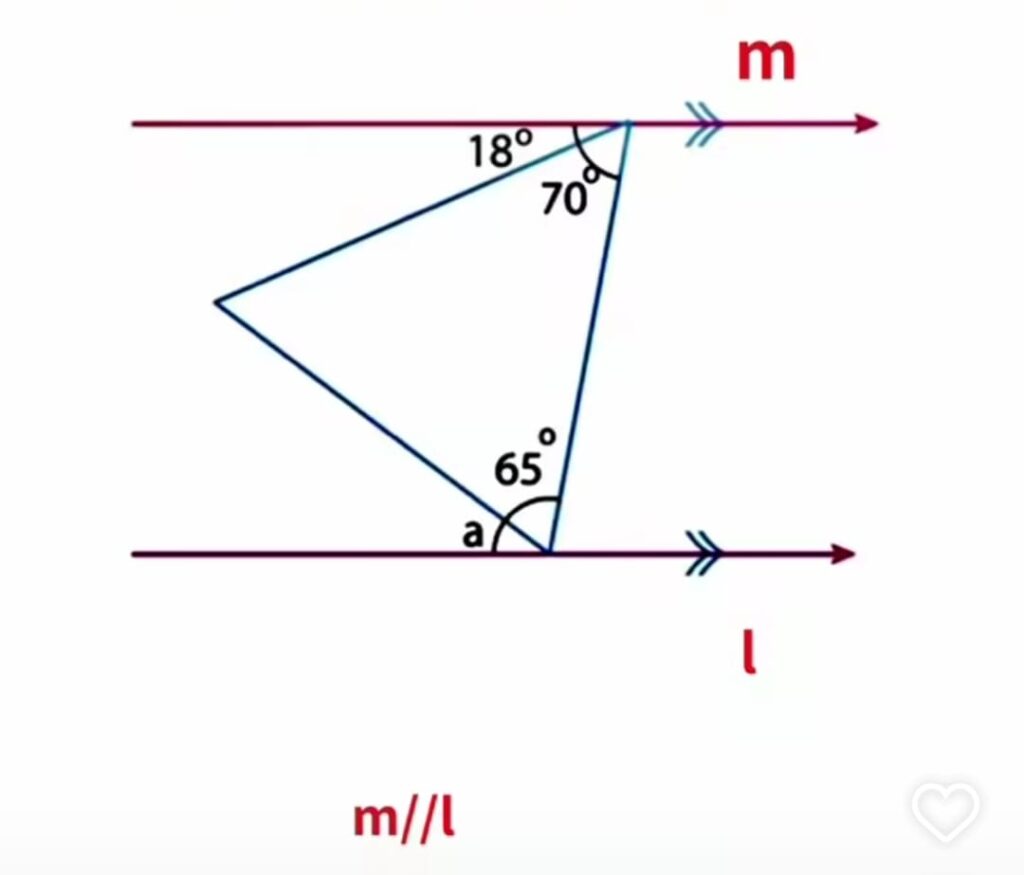
Na figura abaixo, as retas m e l são paralelas (m∥l), e uma transversal forma diferentes ângulos com essas retas. Sabe-se que o ângulo superior adjacente na transversal mede 18°, e o ângulo interno adjacente na base mede 65°. Determine a medida do ângulo a, utilizando as propriedades de ângulos em retas paralelas.
Alternativas:
a) 27°
b) 35°
c) 45°
d) 115°
Ver Solução
Solução Passo a Passo
1. Análise inicial:
Sabemos que m∥l, ou seja, as retas são paralelas, e há uma transversal cortando ambas, formando ângulos co-internos. Esses ângulos co-internos possuem uma propriedade: a soma deles é igual a 180°
2. Identificação dos ângulos co-internos:
Os ângulos co-internos considerados aqui são:
(a + 65°) e (18° + 70°)
3. Aplicação da propriedade dos ângulos co-internos:
Somamos os ângulos co-internos e igualamos a 180°:
(a + 65°) + (18° + 70°) = 180°
4. Resolvendo a equação:
Primeiro, somamos os valores dos ângulos conhecidos:
18° + 70° = 88°.
Substituímos na equação:
a + 65° + 88° = 1 80
Simplificamos:
a + 153° = 180°
Isolamos a:
a = 180° − 153°
a = 27°
5. Conclusão:
A medida do ângulo aa é 27°
Gostou dessa questão? Que tal desafiar ainda mais seus conhecimentos? Clique aqui e resolva outra questão matemática preparada especialmente para você! 📚✨
👉Entre no nosso canal do WhatsApp
Veja mais exercícios de geometria Plana
🟢Mapas Mentais de Matemática para Concurso
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
Pronto para mergulhar em mais desafios matemáticos? 🚀 Explore nossa categoria completa com diversas questões matemática para testar e aprimorar seus conhecimentos! Clique aqui e comece agora! 📘✔️”