Na matemática básica, o estudo das grandezas proporcionais, da regra de três e da porcentagem é fundamental para resolver problemas cotidianos que envolvem comparações, previsões e cálculos financeiros. Este artigo explorará esses conceitos com exemplos práticos e resolvidos, facilitando a compreensão e aplicação no dia a dia.
Grandezas Diretamente Proporcionais
Grandezas diretamente proporcionais são aquelas em que o aumento de uma provoca o aumento da outra na mesma proporção. A relação entre essas grandezas pode ser expressa pela fórmula y = kx, onde k é a constante de proporcionalidade.
Exemplo 1:
Uma fábrica produz 100 peças em 2 horas. Quantas peças a fábrica produzirá em 5 horas?
Solução:
Aqui, a quantidade de peças produzidas é diretamente proporcional ao tempo de produção. Usando a proporção:
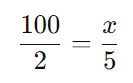
Multiplicando cruzado:
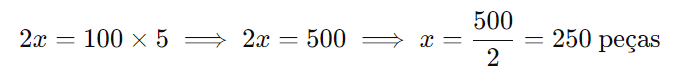
Portanto, a fábrica produzirá 250 peças em 5 horas.
Exemplo 2:
Se um carro percorre 60 km em 1 hora, quantos quilômetros ele percorrerá em 3 horas?
Solução:
A distância percorrida é diretamente proporcional ao tempo. Assim:
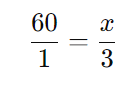
Multiplicando cruzado:

O carro percorrerá 180 km em 3 horas.
Grandezas Inversamente Proporcionais
Grandezas inversamente proporcionais são aquelas em que o aumento de uma provoca a diminuição da outra na mesma proporção. A relação entre essas grandezas é dada por y = k/x.
Exemplo 1:
Se 4 trabalhadores conseguem pintar uma casa em 6 dias, quantos dias levarão 8 trabalhadores para pintar a mesma casa?
Solução:
Aqui, o número de trabalhadores é inversamente proporcional ao tempo necessário:
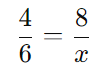
Multiplicando cruzado:
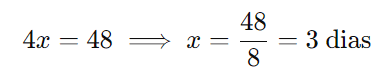
Portanto, 8 trabalhadores levarão 3 dias para pintar a casa.
Exemplo 2:
Se uma torneira enche um tanque em 20 minutos, quanto tempo levarão 4 torneiras para encher o mesmo tanque?
Solução:
O tempo necessário é inversamente proporcional ao número de torneiras:
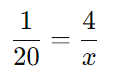
Multiplicando cruzado:
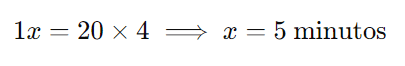
As 4 torneiras juntas encherão o tanque em 5 minutos.
Regra de Três Simples
A regra de três simples é uma técnica usada para resolver problemas que envolvem grandezas proporcionais. Pode ser direta ou inversa, dependendo da relação entre as grandezas.
Exemplo 1:
Uma receita para 4 pessoas leva 200g de arroz. Quanto de arroz será necessário para uma refeição para 10 pessoas?
Solução:
As grandezas (quantidade de arroz e número de pessoas) são diretamente proporcionais:
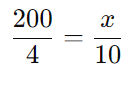
Multiplicando cruzado:
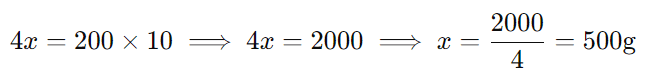
Serão necessários 500g de arroz para 10 pessoas.
Exemplo 2:
Uma viagem de 300 km é feita em 4 horas. Quanto tempo levará uma viagem de 450 km, mantendo a mesma velocidade?
Solução:
As grandezas (distância e tempo) são diretamente proporcionais:
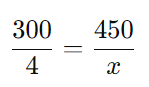
Multiplicando cruzado:
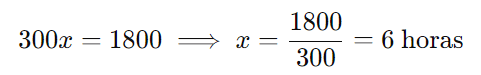
A viagem de 450 km levará 6 horas.
Porcentagem
A porcentagem é uma forma de expressar uma proporção em relação a 100. É amplamente utilizada em contextos financeiros, descontos, juros e muitos outros.
Exemplo 1:
Se um produto custa 200 reais e está com um desconto de 15%, qual será o preço final?
Solução:
Primeiro, calculamos o valor do desconto:
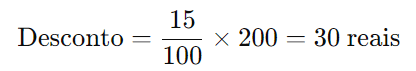
Agora, subtraímos o desconto do preço original:
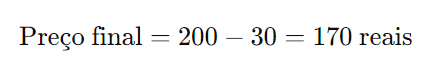
Exemplo 2:
Um salário de 1500 reais foi aumentado em 10%. Qual é o novo salário?
Solução:
Primeiro, calculamos o valor do aumento:
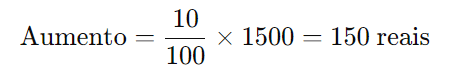
Agora, somamos o aumento ao salário original:
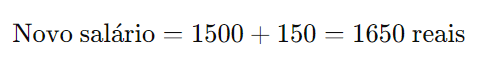
Esses conceitos de grandezas proporcionais, regra de três simples e porcentagem são ferramentas poderosas para resolver uma ampla gama de problemas matemáticos e do dia a dia. A prática com exemplos, como os apresentados, ajudará a fortalecer o entendimento e a aplicação desses conceitos em diversas situações.
Lista de Exercício Grandezas, Regra de Três e Porcentagem
1. Se 5 metros de tecido custam 100 reais, quanto custarão 8 metros?
- (A) 160 reais
- (B) 150 reais
- (C) 140 reais
- (D) 180 reais
2. Um carro percorre 120 km em 2 horas. Quantos quilômetros ele percorrerá em 5 horas na mesma velocidade?
- (A) 200 km
- (B) 250 km
- (C) 300 km
- (D) 350 km
3. Se 3 litros de suco servem 9 pessoas, quantos litros serão necessários para servir 15 pessoas?
- (A) 4 litros
- (B) 5 litros
- (C) 6 litros
- (D) 7 litros
4. Se 8 trabalhadores constroem uma parede em 12 dias, quantos dias levarão 6 trabalhadores para construir a mesma parede?
- (A) 10 dias
- (B) 14 dias
- (C) 16 dias
- (D) 18 dias
5. Uma loja oferece um desconto de 20% em um produto que custa 500 reais. Qual é o preço final do produto?
- (A) 380 reais
- (B) 400 reais
- (C) 420 reais
- (D) 450 reais
6. Se 12 carros saem de uma fábrica em 3 dias, quantos carros sairão em 10 dias?
- (A) 30 carros
- (B) 36 carros
- (C) 40 carros
- (D) 50 carros
7. Se um funcionário ganha 1500 reais por mês e recebe um aumento de 10%, qual será o seu novo salário?
- (A) 1550 reais
- (B) 1600 reais
- (C) 1650 reais
- (D) 1700 reais
8. Se 9 metros de fita custam 27 reais, quanto custam 15 metros?
- (A) 35 reais
- (B) 40 reais
- (C) 45 reais
- (D) 50 reais
9. Se 5 maçãs custam 8 reais, quantas maçãs você pode comprar com 24 reais?
- (A) 10 maçãs
- (B) 12 maçãs
- (C) 15 maçãs
- (D) 20 maçãs
10. Um tanque de água leva 30 minutos para encher com uma torneira. Quanto tempo levarão 3 torneiras para encher o tanque?
- (A) 5 minutos
- (B) 10 minutos
- (C) 15 minutos
- (D) 20 minutos
11. Se um aluno acertou 80% das 50 questões de uma prova, quantas questões ele acertou?
- (A) 30 questões
- (B) 35 questões
- (C) 40 questões
- (D) 45 questões
12. Um desconto de 25% é aplicado em um produto que custa 200 reais. Qual é o valor do desconto?
- (A) 40 reais
- (B) 50 reais
- (C) 60 reais
- (D) 70 reais
13. Se 7 operários levam 14 dias para construir uma estrada, em quantos dias 10 operários farão o mesmo trabalho?
- (A) 8 dias
- (B) 9 dias
- (C) 10 dias
- (D) 11 dias
14. Se 15 livros custam 300 reais, quanto custam 25 livros?
- (A) 400 reais
- (B) 450 reais
- (C) 500 reais
- (D) 550 reais
15. Se um relógio adianta 2 minutos a cada hora, quanto ele adiantará em 6 horas?
- (A) 10 minutos
- (B) 12 minutos
- (C) 14 minutos
- (D) 16 minutos
16. Se 4 caixas pesam 32 kg, quanto pesam 7 caixas?
- (A) 48 kg
- (B) 52 kg
- (C) 56 kg
- (D) 64 kg
17. Um aumento de 15% é aplicado a um salário de 1200 reais. Qual é o novo salário?
- (A) 1320 reais
- (B) 1350 reais
- (C) 1380 reais
- (D) 1400 reais
18. Se 3 metros de tecido custam 90 reais, quanto custam 8 metros?
- (A) 210 reais
- (B) 220 reais
- (C) 230 reais
- (D) 240 reais
19. Se 5 pessoas dividem 500 reais igualmente, quanto cada uma recebe?
- (A) 80 reais
- (B) 90 reais
- (C) 100 reais
- (D) 110 reais
20. Se 80% de uma turma de 50 alunos passou no exame, quantos alunos passaram?
- (A) 35 alunos
- (B) 40 alunos
- (C) 45 alunos
- (D) 50 alunos
Gabarito:
- (A) 160 reais
- (C) 300 km
- (C) 6 litros
- (C) 16 dias
- (B) 400 reais
- (C) 40 carros
- (C) 1650 reais
- (C) 45 reais
- (C) 15 maçãs
- (C) 15 minutos
- (C) 40 questões
- (B) 50 reais
- (B) 9 dias
- (C) 500 reais
- (B) 12 minutos
- (C) 56 kg
- (C) 1380 reais
- (D) 240 reais
- (C) 100 reais
- (B) 40 alunos













