Elipse: Conceito, Propriedades e Equações

A elipse é uma figura geométrica fascinante que surge em diversas áreas da matemática, física e astronomia. Ela é definida como o conjunto de todos os pontos P(x, y) para os quais a soma das distâncias até dois pontos fixos, chamados de focos, é constante.

Elementos da Elipse

1. Centro (O): O ponto central da elipse, equidistante dos focos e dos extremos dos eixos maior e menor.
2. Eixo Maior (A₁A₂): A maior distância entre dois pontos da elipse, passando pelos focos. A medida do eixo maior é 2a, onde a é o semi-eixo maior.
3. Eixo Menor (B₁B₂): A menor distância entre dois pontos da elipse, perpendicular ao eixo maior. A medida do eixo menor é 2b, onde b é o semi-eixo menor.
4. Focos (F₁ e F₂): Dois pontos fixos localizados ao longo do eixo maior. A distância entre os focos é chamada de distância focal, denotada por 2c, onde c é a metade da distância focal.
5. Excentricidade (e): Uma medida que indica o grau de achatamento da elipse, dada por e=c/a​. A excentricidade varia entre 0 (quando a elipse é um círculo, ou seja, c=0) e 1 (quando a elipse se aproxima de uma parábola).

Relação entre a, b e c:

Na elipse, existe uma relação fundamental entre os semi-eixos a, b e a distância focal c, dada por:

Equações da Elipse

A equação geral de uma elipse depende da orientação do seu eixo maior.

1. Eixo Maior Horizontal

Se o eixo maior está orientado horizontalmente, a equação da elipse é dada por:

Neste caso:

• O centro da elipse é o ponto O(0,0).
• Os focos F₁ e F₂ estão localizados em F₁(−c,0) e F₂(c,0).
• O eixo maior é o segmento de reta que vai de A₁(−a,0) até A₂(a,0).
• O eixo menor é o segmento de reta que vai de B₁(0,−b) até B₂(0,b).

Exemplo: Considere uma elipse com centro na origem O(0,0), com semi-eixo maior a=5 e semi-eixo menor b=3. Determine a equação da elipse e as coordenadas dos focos.

Solução:

1. Equação da elipse: A equação de uma elipse com eixo maior horizontal é:

Substituindo a=5 e b=3, temos a equação da elipse abaixo

Para as coordenadas do foco, calculamos a distância focal c usando a relação c² = a² − b²:

Portanto, as coordenadas dos focos são F₁(−4,0) e F₂(4,0).

2. Eixo Maior Vertical

Se o eixo maior está orientado verticalmente, a equação da elipse é dada por:

Neste caso:

• O centro da elipse é o ponto O(0,0).
• Os focos F₁ e F₂ estão localizados em F₁(0,−c) e F₂(0,c).
• O eixo maior é o segmento de reta que vai de A₁(0,−a) até A₂(0,a).
• O eixo menor é o segmento de reta que vai de B₁(−b,0) até B₂(b,0).

Quando o centro da elipse está em O(x₀,y₀), em vez da origem, as equações da elipse são ajustadas para refletir essa translação. Abaixo, apresento as equações para os casos de eixo maior horizontal e vertical.

Exemplo: Considere uma elipse com centro na origem O(0,0), com semi-eixo maior a=7 e semi-eixo menor b=4. Determine a equação da elipse e as coordenadas dos focos.

Solução:

1. Equação da elipse: A equação de uma elipse com eixo maior vertical é:

Substituindo a=7 e b=4, temos a equação da elipse abaixo.

Para as coordenadas do foco, calculamos a distância focal c usando a relação c² = a² − b²:

As coordenadas dos focos são F₁(0, −√33) e F₂(0, √33)

1. Eixo Maior Horizontal

Se o eixo maior está orientado horizontalmente e o centro da elipse é O(x₀,y₀), a equação da elipse é:

Neste caso:

• O centro da elipse é o ponto O(x₀,y₀).
• Os focos F₁ e F₂ estão localizados em F₁(x₀−c, y₀) e F₂(x₀+c,y₀).
• O eixo maior é o segmento de reta que vai de A₁(x₀−a,y₀) até A₂(x₀+a,y₀).
• O eixo menor é o segmento de reta que vai de B₁(x₀,y₀−b) até B₂(x₀,y₀+b).

Exemplo: Considere uma elipse com centro em O(2,−3), com semi-eixo maior a=6 e semi-eixo menor b=4. Determine a equação da elipse e as coordenadas dos focos.

A equação de uma elipse com eixo maior horizontal e centro O(x₀,y₀) é:

Substituindo x₀=2, y₀=−3, a=6a = 6 e b=4:

Para as coordenadas do foco, calculamos a distância focal c:

As coordenadas dos focos são F₁(2−√20,−3) e F₂(2+√20,−3).

2. Eixo Maior Vertical

Se o eixo maior está orientado verticalmente e o centro da elipse é O(x₀,y₀), a equação da elipse é:

Neste caso:

• O centro da elipse é o ponto O(x₀, y₀).
• Os focos F₁ e F₂ estão localizados em F₁(x₀, y₀−c) e F₂(x₀, y₀+c).
• O eixo maior é o segmento de reta que vai de A₁(x₀, y₀−a) até A₂(x₀, y₀+a).
• O eixo menor é o segmento de reta que vai de B₁(x₀−b, y₀) até B₂(x₀+b, y₀).

Exemplo: Considere uma elipse com centro em O(−1, 4), com semi-eixo maior a=8 e semi-eixo menor b=6. Determine a equação da elipse e as coordenadas dos focos.

Substituindo x₀=−1, y₀=4, a=8 e b=6 em

temos a equação da elipse.

para o foco, calculamos a distância focal c:

As coordenadas dos focos são F₁(−1, 4−√28) e F₂(−1,4+√28).

Propriedades Importantes

Relação entre a, b e c:

Na elipse, existe uma relação fundamental entre os semi-eixos a, b e a distância focal c, dada por:

Isso implica que, para calcular a excentricidade e, podemos usar:

Comprimento da Elipse:

O perímetro de uma elipse não possui uma fórmula simples, mas pode ser aproximado pela fórmula de Ramanujan:

Área da Elipse:

A área de uma elipse é dada por:

Onde a é o semi-eixo maior e b é o semi-eixo menor.

Aplicações da Elipse

As elipses aparecem em diversos contextos, como na descrição das órbitas planetárias (Lei de Kepler), em antenas parabólicas, e até em arquitetura e arte.

Conclusão

A elipse é uma das cônicas mais ricas em propriedades geométricas e aplicações práticas. Com suas equações e características específicas, ela é essencial para entender muitos fenômenos naturais e artificiais. Estudar a elipse, portanto, é essencial para aprofundar-se na geometria analítica e nas aplicações que se estendem muito além das salas de aula.

Leia também

Geometria Analítica: Pontos ⇒ Distância, Ponto Médio e Colinearidade

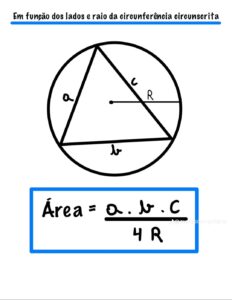
Distância entre Retas e Cálculo da Área de um Triângulo

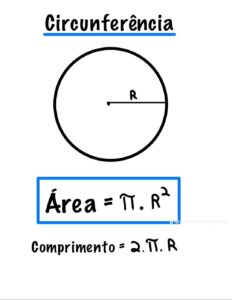
Circunferência: Equação Geral e Reduzida

A Parábola: Definição, Propriedades e Equações 

Elipse: Conceito, Propriedades e Equações

Hipérbole: Um Guia Completo