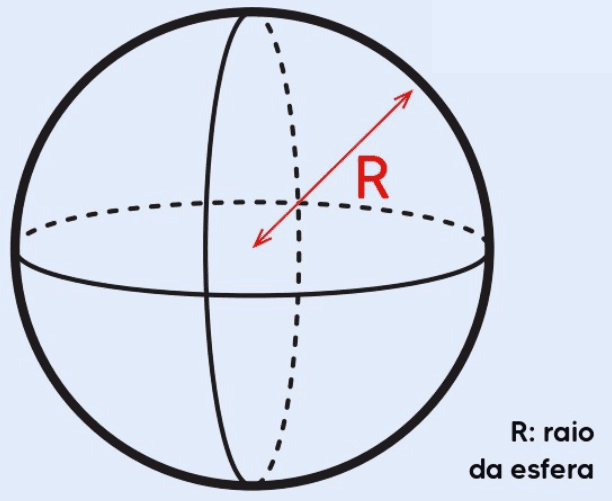
A esfera é uma das formas geométricas mais fascinantes e fundamentais na matemática e na física. Ela é definida como o conjunto de todos os pontos que estão a uma distância constante (raio) de um ponto central em um espaço tridimensional. Neste artigo, exploraremos várias propriedades e conceitos relacionados à esfera, incluindo seu volume, área total, secção, fuso esférico, cunha esférica e suas respectivas áreas e volumes.
Volume da Esfera
O volume de uma esfera é dado pela fórmula:

onde:
- V é o volume da esfera.
- R é o raio da esfera.
Essa fórmula nos dá a quantidade de espaço que a esfera ocupa em um espaço tridimensional.
Exemplo: Calcule o volume de uma esfera com raio R=5cm.
Solução: Usamos a fórmula do volume:
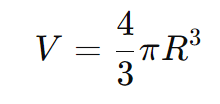
Substituindo R=5cm:
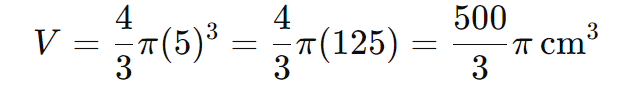
Aproximando o valor de π como 3,14:
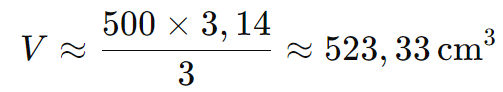
Portanto, o volume da esfera é aproximadamente 523,33 cm³
Área Total da Esfera
A área da superfície de uma esfera é calculada usando a seguinte fórmula:
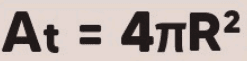
onde:
- A é a área total da esfera.
- R é o raio da esfera.
Essa é a área da “casca” da esfera, que cobre toda a superfície externa.
Exemplo: Calcule a área da superfície de uma esfera com raio R=7m.
Solução: Usamos a fórmula da área total:
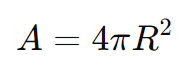
Substituindo R=7m:

Aproximando π como 3,14:
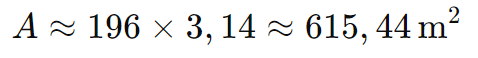
Portanto, a área da superfície da esfera é aproximadamente 615,44 m².
Secção Esférica
Uma secção esférica é a intersecção de uma esfera com um plano. Se o plano passa pelo centro da esfera, a secção resultante é um círculo máximo, cujo raio é igual ao raio da esfera (R). Se o plano não passa pelo centro, a secção é um círculo menor, com raio (r) determinado pela fórmula:

onde:
- r é o raio da secção.
- R é o raio da esfera.
- d é a distância entre a secção e o centro da esfera.

Exemplo: Uma esfera de raio R=10cm é cortada por um plano a uma distância d=6 cm do centro. Qual é o raio r da secção?
Solução: Usamos a fórmula do raio da secção:

Substituindo R=10cm e d=6 cm:

Portanto, o raio da secção é 8 cm.
Fuso Esférico
Um fuso esférico é uma região da superfície da esfera limitada por dois meridianos que se encontram nos polos da esfera. Ele pode ser visualizado como a “fatia” de uma esfera delimitada por um ângulo α no centro da esfera.

Área do Fuso Esférico
A área de um fuso esférico é proporcional ao ângulo α (em graus) que ele subtende no centro da esfera:

Utilizando o ângulo em radiano temos:
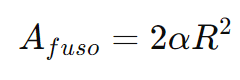
onde:
- A é a área do fuso esférico.
- α é o ângulo de abertura do fuso, medido em graus ou radiano.
- R é o raio da esfera.
Exemplo: Calcule a área de um fuso esférico em uma esfera de raio R=3 m, sabendo que o ângulo de abertura απ é π/4 radianos.
Solução:
Usamos a fórmula da área do fuso:

Substituindo α=π/4 e R=3m:
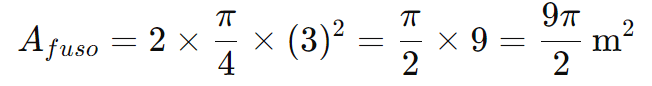
Aproximando π como 3,14:

Portanto, a área do fuso esférico é aproximadamente 14,13 m².
Cunha Esférica
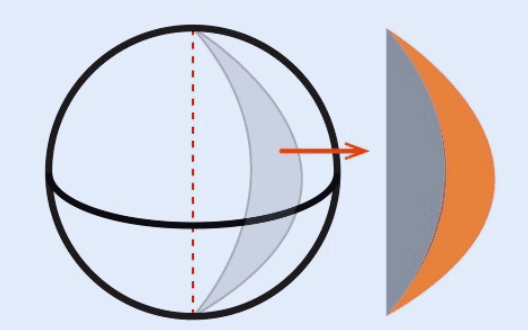
Uma cunha esférica é a região tridimensional da esfera delimitada por dois planos que passam pelo centro da esfera, formando um ângulo α entre eles. Ela pode ser vista como a “fatia” tridimensional correspondente ao fuso esférico.
Volume da Cunha Esférica
O volume de uma cunha esférica é dado por:

Utilizando o ângulo em radiano temos:
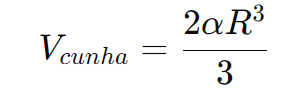
onde:
- V é o volume da cunha esférica.
- α é o ângulo de abertura da cunha, medido em graus ou radianos.
- R é o raio da esfera.
Exemplo: Determine o volume de uma cunha esférica em uma esfera com raio R=4cm, onde o ângulo α π/3 radianos.
Solução: Usamos a fórmula do volume da cunha:
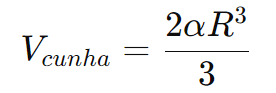
Substituindo α=π/3 e R=4cm:

Aproximando π como 3,14:
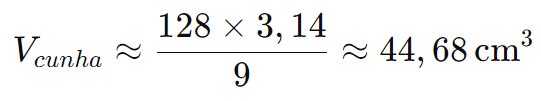
Portanto, o volume da cunha esférica é aproximadamente 44,68 cm³.
Área da Cunha Esférica
A área da superfície lateral da cunha esférica, que corresponde à área do fuso esférico, é dada por:

onde:
- A é a área da superfície lateral da cunha esférica.
- α é o ângulo de abertura da cunha, medido em graus.
- R é o raio da esfera.
Exemplo: Encontre a área da superfície lateral de uma cunha esférica em uma esfera de raio R=6m, onde o ângulo α é π/6 radianos.
Solução: Usamos a fórmula da área da cunha:

Substituindo α=π/6 e R=6m:

Aproximando π como 3,14:

Portanto, a área da superfície lateral da cunha esférica é aproximadamente 37,68 m².
Conclusão
A esfera é uma figura geométrica rica em propriedades matemáticas. Compreender o volume, a área, as secções e as regiões como fusos e cunhas esféricas é fundamental para aplicações em diversas áreas da ciência e da engenharia. As fórmulas apresentadas fornecem as bases necessárias para explorar esses conceitos em profundidade.
Leia também
O Cubo: Propriedades e Fórmulas Essenciais
O Paralelepípedo: Propriedades e Fórmulas Essenciais
Pirâmides: Propriedades, Fórmulas e Aplicações
Tetraedro Regular: Propriedades, Fórmulas e Aplicações
Tronco de Pirâmide: Propriedades, Fórmulas e Proporções
Cilindro: Conceitos e Cálculos
Cone: Tudo o Que Você Precisa Saber
Poliedros: Estrutura, Teorema de Euler e Poliedros de Platão













