Os ângulos são elementos fundamentais da geometria e têm um papel essencial em diversas áreas da matemática e ciências aplicadas. Compreender os diferentes tipos de ângulos e suas propriedades é crucial para uma base sólida em geometria. Neste artigo, exploraremos os quatro tipos principais de ângulos: agudo, obtuso, reto e raso.
1. Ângulo Agudo
Definição: Um ângulo agudo é aquele que mede menos de 90 graus.
Características:
- A medida está entre 0 e 90 graus.
- Ângulos agudos são mais “pontudos” e são frequentemente encontrados em triângulos agudos, onde todos os ângulos são agudos.
- Exemplos do mundo real incluem a ponta de um lápis ou o ângulo formado pelas pernas de uma mesa inclinada.
Como Identificar: Para identificar um ângulo agudo, você pode usar um transferidor para medir o ângulo. Se a medida for menor que 90 graus, é um ângulo agudo.

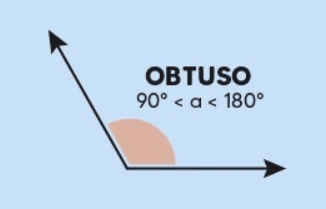
2. Ângulo Obtuso
Definição: Um ângulo obtuso é aquele cuja medida está entre 90 e 180 graus.
Características:
- A medida está entre 90 e 180 graus.
- Ângulos obtusos são mais “abertos” e são encontrados em triângulos obtusos, onde um dos ângulos é obtuso.
- Exemplos incluem a abertura de uma porta quando é empurrada mais do que a metade do caminho ou a inclinação de uma rampa.
Como Identificar: Use um transferidor para medir o ângulo. Se a medida estiver entre 90 e 180 graus, é um ângulo obtuso.
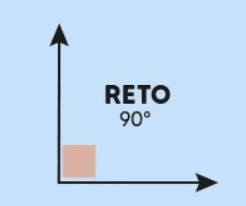
3. Ângulo Reto
Definição: Um ângulo reto é um ângulo que mede exatamente 90 graus.
Características:
- É o ângulo padrão que forma um quadrado ou um retângulo.
- Ângulos retos são perpendiculares e estão presentes em estruturas como portas e janelas.
- São fundamentais na construção de figuras geométricas e na definição de formas regulares.
Como Identificar: O ângulo reto pode ser identificado com um esquadro ou medido com um transferidor. A marca de um ângulo reto é frequentemente representada por um pequeno quadrado no vértice do ângulo.
4. Ângulo Raso
Definição: Um ângulo raso é aquele que mede exatamente 180 graus.
Características:
- Forma uma linha reta e é chamado de “ângulo plano”.
- Ângulos rasos não formam um “v” ou qualquer outro tipo de abertura; eles se estendem em linha reta.
- Exemplos incluem a linha formada pelas mãos de um relógio quando estão às 12 horas ou uma linha reta em uma folha de papel.
Como Identificar: Se a medida do ângulo for exatamente 180 graus, então é um ângulo raso. Em figuras planas, um ângulo raso aparece como uma linha reta contínua.

Resumo sobre Ângulos: Agudo, Obtuso, Reto e Raso
Os ângulos são fundamentais na geometria e são classificados principalmente em quatro tipos:
- Ângulo Agudo: Mede menos de 90 graus. É um ângulo “pontudo” encontrado em triângulos agudos.
- Ângulo Obtuso: Mede entre 90 e 180 graus. É um ângulo “aberto” encontrado em triângulos obtusos.
- Ângulo Reto: Mede exatamente 90 graus. É o ângulo padrão em figuras como quadrados e retângulos, formando uma linha perpendicular.
- Ângulo Raso: Mede exatamente 180 graus. Forma uma linha reta e é também conhecido como ângulo plano.
Cada tipo de ângulo tem suas características e aplicações práticas, desempenhando um papel crucial em diversas áreas da matemática e design.

Conclusão
Compreender os diferentes tipos de ângulos é fundamental para resolver problemas geométricos e entender a matemática espacial. Cada tipo de ângulo tem suas próprias características e aplicações práticas no mundo real. Seja ao projetar um edifício, desenhar uma forma ou simplesmente analisar a arquitetura ao nosso redor, o conhecimento sobre ângulos ajuda a entender e aplicar a matemática de maneira eficaz.
Ângulos Complementares e Suplementares
Os ângulos são uma parte fundamental da geometria, e entender os diferentes tipos e suas relações é crucial para muitas aplicações matemáticas e práticas. Dois conceitos importantes relacionados a ângulos são os ângulos complementares e suplementares. Neste artigo, exploraremos esses conceitos em detalhes, explicando suas definições, propriedades e aplicações práticas.
1. Ângulos Complementares
Definição: Dois ângulos são chamados de complementares quando a soma de suas medidas é exatamente 90 graus.
Características:
- Se você adicionar a medida de dois ângulos e o total for 90 graus, esses ângulos são complementares.
- Exemplos de pares de ângulos complementares incluem 30 graus e 60 graus, ou 45 graus e 45 graus.
- Ângulos complementares podem estar adjacentes (compartilhando um lado comum) ou não adjacentes.
Propriedades:
- Ângulos complementares são frequentemente encontrados em várias figuras geométricas e problemas matemáticos.
- Em um triângulo retângulo, os dois ângulos agudos são sempre complementares, já que o ângulo reto soma 90 graus com eles.

Aplicações Práticas:
- Arquitetura e Design: Usados para criar ângulos específicos e garantir a precisão em projetos.
- Engenharia: Em cálculos de estruturas e componentes que precisam se encaixar corretamente.
Exemplo: Se um ângulo mede 40 graus, seu ângulo complementar é 50 graus, pois 40 + 50 = 90 graus.
Exercício 1: Ângulos Complementares
Problema: Encontre o ângulo complementar de um ângulo que mede 35 graus.
Solução:
- Definição de Ângulos Complementares: Dois ângulos são complementares se a soma de suas medidas for 90 graus.
- Cálculo: Para encontrar o ângulo complementar, subtraia a medida do ângulo dado de 90 graus. Ângulo complementar = 90° − 35° = 55∘
Resposta: O ângulo complementar é 55 graus.
2. Ângulos Suplementares
Definição: Dois ângulos são chamados de suplementares quando a soma de suas medidas é exatamente 180 graus.
Características:
- Se você adicionar a medida de dois ângulos e o total for 180 graus, esses ângulos são suplementares.
- Exemplos de pares de ângulos suplementares incluem 110 graus e 70 graus, ou 90 graus e 90 graus.
- Ângulos suplementares podem ser adjacentes (formando uma linha reta) ou não adjacentes.
Propriedades:
- Ângulos suplementares são comuns em figuras planas e cálculos geométricos.
- Em um triângulo, a soma dos ângulos internos é sempre 180 graus, portanto, qualquer dois ângulos internos de um triângulo são suplementares com o terceiro ângulo.

Aplicações Práticas:
- Construção e Carpintaria: Usados para medir e ajustar ângulos em projetos.
- Navegação e Mapas: Ajuda na leitura e interpretação de ângulos em cartas náuticas e mapas.
Exemplo: Se um ângulo mede 120 graus, seu ângulo suplementar é 60 graus, pois 120 + 60 = 180 graus.
Exercício 2: Ângulos Suplementares
Problema: Determine o ângulo suplementar de um ângulo que mede 122 graus.
Solução:
- Definição de Ângulos Suplementares: Dois ângulos são suplementares se a soma de suas medidas for 180 graus.
- Cálculo: Para encontrar o ângulo suplementar, subtraia a medida do ângulo dado de 180 graus.
- Ângulo suplementar= 180°−122° = 58°
Resposta: O ângulo suplementar é 58 graus.
Conclusão
Os conceitos de ângulos complementares e suplementares são fundamentais para resolver muitos problemas geométricos e aplicar a matemática a situações do mundo real. Compreender como esses ângulos interagem e como calcular seus pares é essencial para a construção, design e muitas outras disciplinas. Saber identificar e aplicar esses conceitos pode melhorar a precisão e a eficiência em uma variedade de tarefas matemáticas e práticas.
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes