(CESPE / CEBRASPE 2024 – Prefeitura de Camaçari – BA – Assistente Administrativo)
Assinale a opção que corresponde ao gráfico da função ƒ(x) = – 12x + 3x2 + 3, no plano xOy.
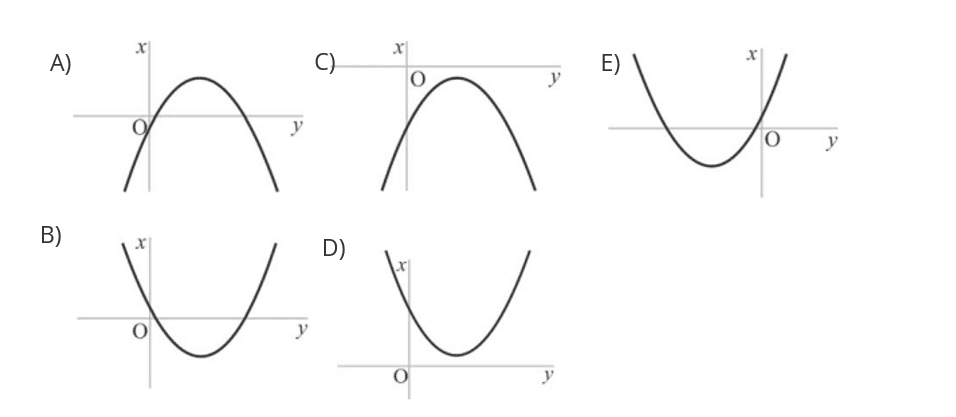
Para determinar o gráfico da função f(x) = -12x + 3x2 + 3, devemos analisar a sua forma e identificar suas características principais, como a concavidade, o vértice e os pontos de interseção com os eixos coordenados.
Análise da Função
A função dada é uma função quadrática da forma:
f(x) = ax2 + bx + c
onde:
- ( a = 3 )
- ( b = -12 )
- ( c = 3 )
Passo 1: Determinar a Concavidade
A concavidade da parábola depende do coeficiente ( a ). Se ( a > 0 ), a parábola é côncava para cima (forma de “U”). Se ( a < 0 ), a parábola é côncava para baixo (forma de “∩”).
Como ( a = 3 > 0 ), a parábola é côncava para cima.
Passo 2: Determinar o Vértice da Parábola
O vértice da parábola é o ponto mais baixo (mínimo) ou mais alto (máximo) da curva, dependendo da concavidade. Para encontrar o vértice, utilizamos as fórmulas:

Substituindo os valores de ( a ) e ( b ):
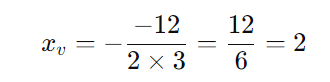
Agora, calculamos ( yv = f(xv) ):

Portanto, o vértice da parábola é (2, -9).
Passo 3: Determinar os Pontos de Interseção com os Eixos Coordenados
- Interseção com o eixo ( y ): ocorre quando ( x = 0 ):
f(0) = 3(0)2 – 12(0) + 3 = 3
Portanto, o ponto de interseção com o eixo ( y ) é (0, 3).
- Interseção com o eixo ( x ): ocorre quando f(x) = 0:
3x2 – 12x + 3 = 0
Dividimos toda a equação por 3:
x2 – 4x + 1 = 0
Usamos a fórmula de Bhaskara para encontrar as raízes:

Neste caso, ( a = 1 ), ( b = -4 ), ( c = 1 ):

Portanto, os pontos de interseção com o eixo ( x ) são:
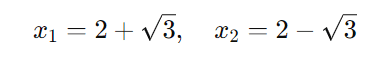
Conclusão sobre o Gráfico
- A parábola é côncava para cima.
- Tem vértice no ponto (2, -9).
- Interseção com o eixo ( y ) em (0, 3).
- Interseções com o eixo ( x ) em (2 + √3, 0) e (2 – √3, 0).
Com essas informações, o gráfico da função é uma parábola côncava para cima que passa pelos pontos indicados.
Com essas informações, o gráfico será:

Alternativa correta Letra B













