Na geometria, os conceitos de inscrição e circunscrição são fundamentais para entender como polígonos regulares se relacionam com circunferências. Neste artigo, exploraremos esses conceitos aplicados a triângulos equiláteros, quadrados e hexágonos regulares, utilizando a notação onde o lado do polígono é representado por a.
Conceitos Fundamentais
- Inscrição: Um polígono é inscrito em uma circunferência quando todos os seus vértices estão sobre a circunferência. A circunferência é então dita circunscrita ao polígono.
- Circunscrição: Um polígono é circunscrito a uma circunferência quando todos os seus lados são tangentes à circunferência. A circunferência é então dita inscrita no polígono.
1. Triângulo Equilátero
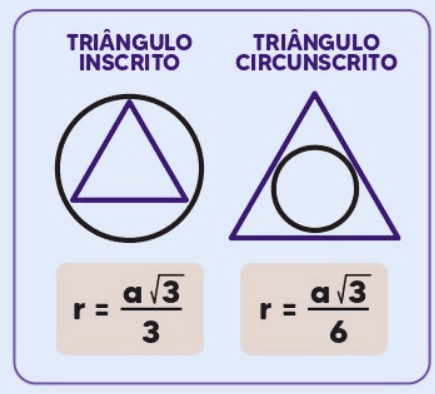
Inscrição de um Triângulo Equilátero em uma Circunferência
Um triângulo equilátero pode ser inscrito em uma circunferência, com todos os seus vértices tocando a circunferência. O raio R da circunferência circunscrita é relacionado ao lado a do triângulo pela fórmula:
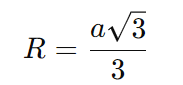
Circunscrição de uma Circunferência em um Triângulo Equilátero
Uma circunferência pode ser inscrita em um triângulo equilátero, tocando todos os seus lados. O raio r da circunferência inscrita é dado pela fórmula:
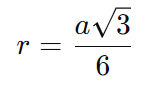
onde a é o comprimento de um lado do triângulo.
2. Quadrado
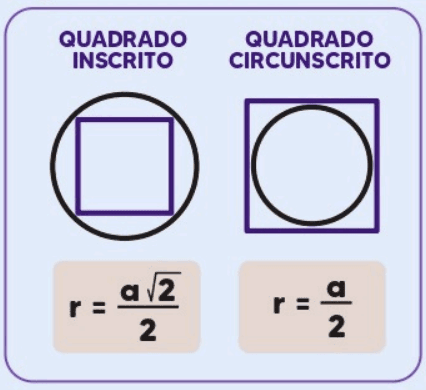
Inscrição de um Quadrado em uma Circunferência
Um quadrado pode ser inscrito em uma circunferência de modo que todos os seus vértices estejam sobre a circunferência. O raio R da circunferência circunscrita é relacionado ao lado a do quadrado pela fórmula:

O centro da circunferência coincide com o centro do quadrado.
Circunscrição de uma Circunferência em um Quadrado
Uma circunferência pode ser inscrita em um quadrado, tocando todos os lados do quadrado. O raio r da circunferência inscrita é metade do lado a do quadrado:
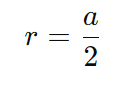
O centro da circunferência também coincide com o centro do quadrado.
3. Hexágono Regular
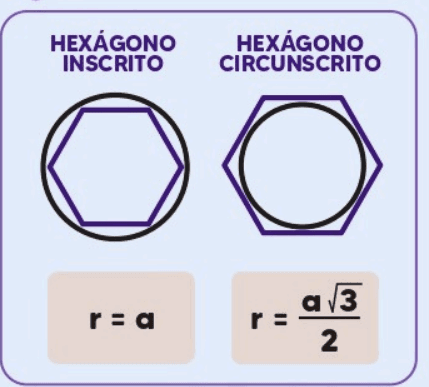
Inscrição de um Hexágono Regular em uma Circunferência
Um hexágono regular pode ser inscrito em uma circunferência, com todos os seus vértices tocando a circunferência. O raio R da circunferência circunscrita é igual ao lado a do hexágono:

qui, o centro do hexágono é também o centro da circunferência.
Circunscrição de uma Circunferência em um Hexágono Regular
Uma circunferência pode ser inscrita em um hexágono regular, tocando todos os seus lados. O raio r da circunferência inscrita é relacionado ao lado a do hexágono pela fórmula:
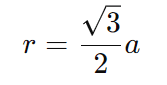
O centro da circunferência coincide com o centro do hexágono.
Resumo: Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Inscrição e Circunscrição referem-se às relações entre polígonos regulares e circunferências:
- Inscrição: O polígono é inscrito em uma circunferência se todos os seus vértices estão sobre a circunferência. A circunferência é chamada de circunscrita ao polígono.
- Circunscrição: O polígono é circunscrito a uma circunferência se todos os seus lados são tangentes à circunferência. A circunferência é chamada de inscrita no polígono.
Triângulo Equilátero:
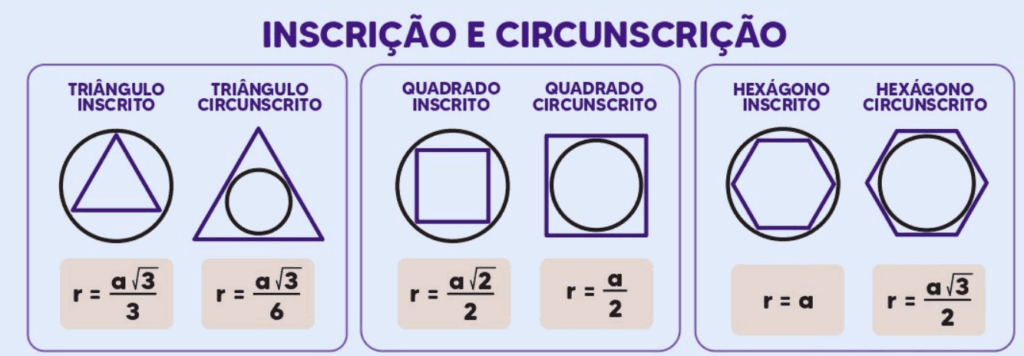
- Inscrição: O triângulo pode ser inscrito em uma circunferência com raio R=a√3/3, onde a é o comprimento do lado.
- Circunscrição: Uma circunferência pode ser inscrita no triângulo com raio r=a√3/6.
Quadrado:
- Inscrição: Um quadrado pode ser inscrito em uma circunferência com raio R=a√2/2.
- Circunscrição: A circunferência inscrita no quadrado tem raio r=a/2.
Hexágono Regular:
- Inscrição: Um hexágono regular pode ser inscrito em uma circunferência com raio R=a, onde a é o comprimento do lado.
- Circunscrição: A circunferência inscrita no hexágono regular tem raio r=a√3/2a.
Esses conceitos são importantes para compreender a relação entre polígonos regulares e circunferências, com aplicações em matemática, design e engenharia.
Conclusão
A inscrição e circunscrição de triângulos equiláteros, quadrados e hexágonos regulares oferecem uma visão profunda sobre as relações entre polígonos e circunferências. Esses conceitos são importantes em diversas áreas da matemática e têm aplicações práticas em design, engenharia e arquitetura.
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes