Pirâmides: Propriedades, Fórmulas e Aplicações

A pirâmide é uma figura geométrica tridimensional da matemática que consiste em uma base poligonal e faces laterais triangulares que se encontram em um ponto comum chamado vértice. As pirâmides podem ter várias formas de base, sendo as mais comuns as bases triangular, quadrada e hexagonal. Neste artigo, abordaremos as propriedades principais dessas pirâmides, incluindo a área da base, área lateral, volume, área total, e exploraremos conceitos como apótema da base e a relação métrica fundamental.

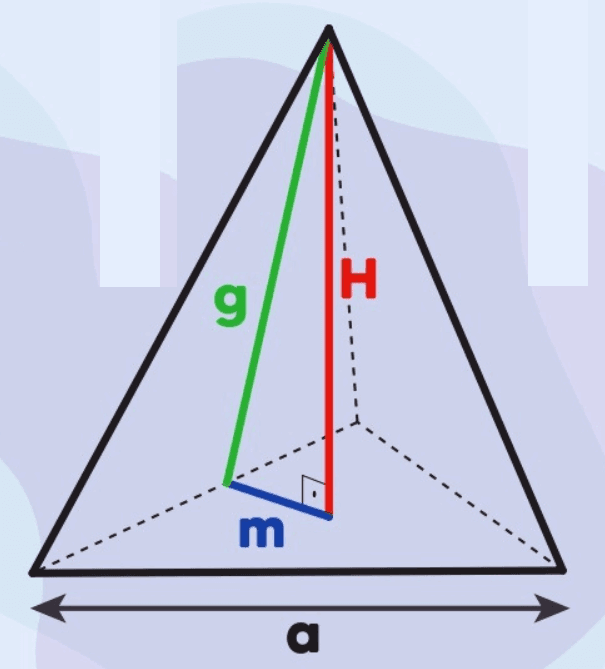
Pirâmide com Base Triangular

• Área da Base (Ab): Para uma pirâmide com base triangular equilátera, onde cada lado da base tem comprimento a, a área da base é dada por:

• Área Lateral (Al): A área lateral é a soma das áreas das três faces laterais triangulares. Se g é o apótema lateral, a área lateral é:

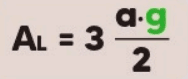
• Volume (V): O volume da pirâmide é calculado como um terço da área da base multiplicada pela altura H:

• Área Total (At): A área total é a soma da área da base com a área lateral:

Pirâmide com Base Quadrada

• Área da Base (Ab): Para uma pirâmide com base quadrada, onde cada lado da base tem comprimento aaa, a área da base é:

• Área Lateral (Al): A área lateral é a soma das áreas das quatro faces laterais triangulares:

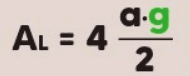
• Volume (V): O volume da pirâmide é:

• Área Total (At): A área total é:

Pirâmide com Base Hexagonal

• Área da Base (Ab): Para uma pirâmide com base hexagonal regular, onde cada lado da base tem comprimento a, a área da base é:

• Área Lateral (Al): A área lateral é a soma das áreas das seis faces laterais triangulares:

• Volume (V): O volume da pirâmide é:

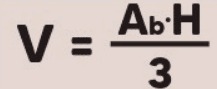
• Área Total (At): A área total é:

Apótema da Base

O apótema da base é a distância do centro da base até o ponto médio de um dos lados da base. Para cada tipo de base, o apótema é calculado da seguinte forma:

• Base Triangular (Equilátero): O apótema m é dado por:

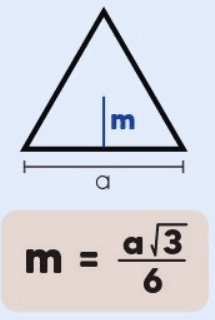
• Base Quadrada: O apótema m é:

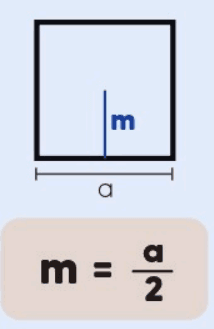
• Base Hexagonal (Regular): O apótema m é:

Relação Métrica: m²+H²=g²

Na geometria das pirâmides, existe uma relação métrica fundamental entre a altura HHH, o apótema da base mmm, e o apótema lateral ggg. Essa relação é expressa pela fórmula:

Essa fórmula é derivada do Teorema de Pitágoras, aplicada ao triângulo retângulo formado pelo apótema da base, a altura da pirâmide e o apótema lateral.

Conclusão

As pirâmides, com suas diversas bases, oferecem uma rica variedade de propriedades geométricas que são essenciais para a compreensão da geometria tridimensional. Desde o cálculo da área da base até a aplicação da relação métrica fundamental, entender esses conceitos permite uma análise completa e precisa das pirâmides e suas aplicações práticas.

Leia também

Prismas: Uma Análise Completa

O Cubo: Propriedades e Fórmulas Essenciais 

O Paralelepípedo: Propriedades e Fórmulas Essenciais

Pirâmides: Propriedades, Fórmulas e Aplicações 

Tetraedro Regular: Propriedades, Fórmulas e Aplicações

Tronco de Pirâmide: Propriedades, Fórmulas e Proporções 

Cilindro: Conceitos e Cálculos

Cone: Tudo o Que Você Precisa Saber

Esfera: Um Estudo Completo 

Poliedros: Estrutura, Teorema de Euler e Poliedros de Platão