O que são “pontos notáveis”?
Chamamos de pontos notáveis do triângulo os pontos definidos pela concorrência (interseção) de segmentos ou retas especiais. Os quatro clássicos são:
- Baricentro (G): encontro das medianas. Medianas e baricentro.
- Incentro (I): encontro das bissetrizes internas. Bissetrizes e incentro.
- Circuncentro (O): encontro das mediatrizes dos lados. Base de congruência.
- Ortocentro (H): encontro das alturas. Alturas e ortocentro.
Cada ponto notável tem interpretação geométrica (centro de massa, círculo inscrito, círculo circunscrito, etc.) e posição que varia conforme o tipo de triângulo.
Artigo atualizado sobre Pontos Notáveis do Triângulo
Medianas e baricentro
Num triângulo ABC, marquemos M1 , ponto médio do lado BC.
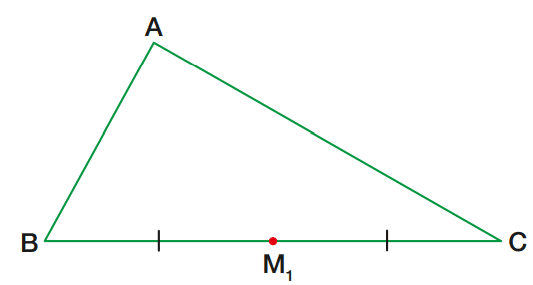
Tracemos o segmento AM1:
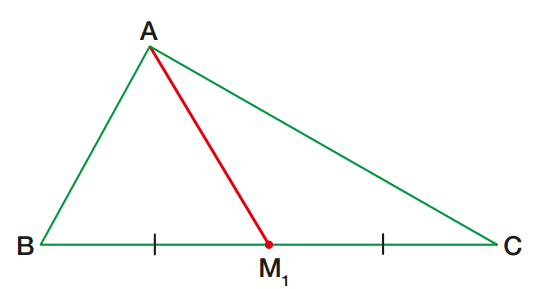
O segmento AM1 é uma mediana do triângulo ABC.
Mediana de um triângulo é um segmento com extremidades num vértice e no ponto médio do lado oposto.
Um triângulo tem três medianas. Na figura, as três medianas são:
- AM1, mediana relativa ao lado BC ou ao vértice A;
- BM2, mediana relativa ao lado AC ou ao vértice B;
- CM3, mediana relativa ao lado AB ou ao vértice C.
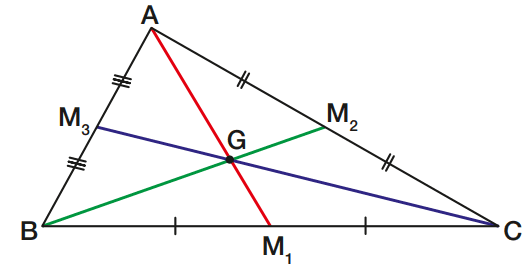
As três medianas de um triângulo encontram-se num ponto chamado baricentro do triângulo.
Na figura acima, G é o baricentro do triângulo ABC.
Bissetrizes e incentro
Num triângulo ABC, tracemos a bissetriz AS1, relativa ao ângulo A. Chamemos de S1 o ponto de encontro da bissetriz com o lado BC.
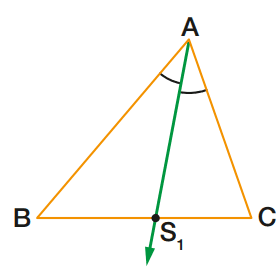
Destaquemos o segmento AS1.
O segmento AS1 é uma bissetriz do triângulo ABC.
Observe que:
- o segmento AS1 está contido na semirreta AS1 (bissetriz do ângulo A);
- S1 é a interseção do lado BC com a bissetriz do ângulo A
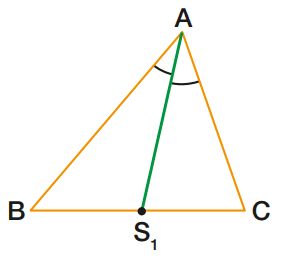
Bissetriz de um triângulo é um segmento com extremidades num vértice e no lado oposto e que divide o ângulo desse vértice em dois ângulos congruentes.
Um triângulo tem três bissetrizes. Na figura, as três bissetrizes são:
- AS1, bissetriz relativa ao lado BC ou ao vértice A;
- BS2, bissetriz relativa ao lado AC ou ao vértice B;
- CS3, bissetriz relativa ao lado AB ou ao vértice C.
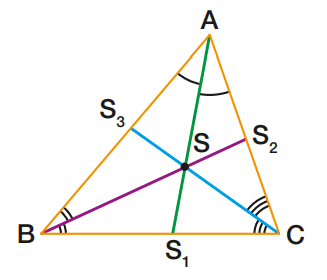
As três bissetrizes de um triângulo encontram-se num ponto chamado incentro do triângulo
Na figura acima, S é o incentro do triângulo ABC.
Alturas e ortocentro
Num triângulo ABC, tracemos pelo ponto A uma reta r perpendicular à reta que contém o lado BC.
A reta que contém o lado BC, reta BC, é chamada de reta suporte do lado BC.
Chamemos de H1 o ponto de encontro da reta r com a reta BC:
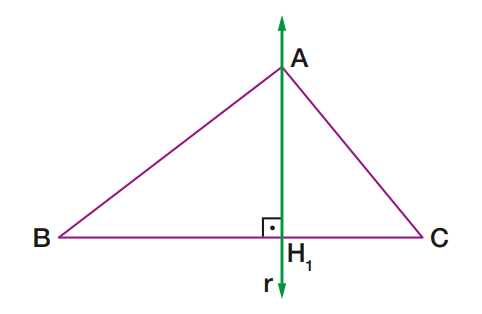
Destaquemos o segmento AH1 :
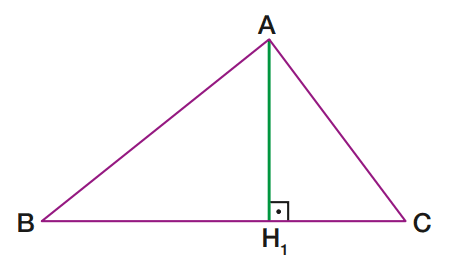
O segmento AH1 é uma altura do triângulo ABC.
O ponto H1 é a interseção da reta BC com a perpendicular a ela conduzida pelo ponto A. H1
também é chamado pé da altura.
Altura de um triângulo é o segmento perpendicular à reta suporte de um lado, com extremidade nessa reta e no vértice oposto a esse lado.
Um triângulo tem três alturas. Observe:
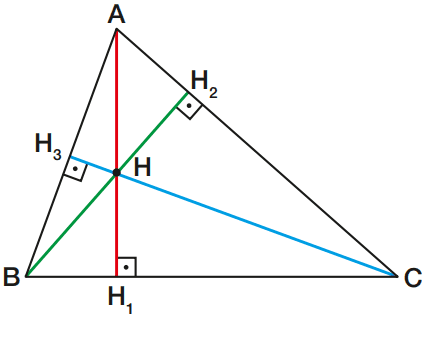
Nas figuras acima, as três alturas são:
- AH1, altura relativa ao lado BC ou ao vértice A;
- BH2 altura relativa ao lado AC ou ao vértice B;
- CH3, altura relativa ao lado AB ou ao vértice C.
As três alturas, ou os seus prolongamentos, encontram-se num ponto chamado ortocentro do triângulo.
Nas figuras acima, H é o ortocentro do triângulo ABC, o qual pode ser interno ao triângulo (quando o triângulo ABC é acutângulo) ou externo ao triângulo (quando o triângulo ABC é obtusângulo).
Mediatrizes e circuncentro
Num triângulo ABC, tracemos a reta m1 perpendicular ao lado BC e passando por M1 , ponto médio de BC:
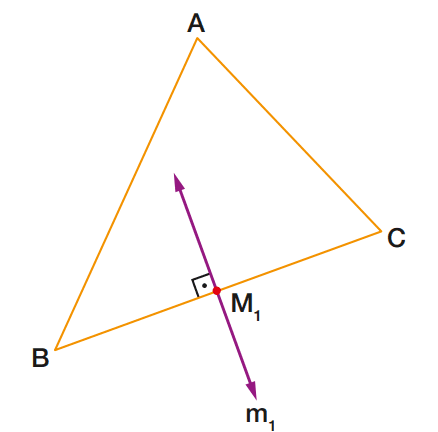
A reta m1 é a mediatriz do lado BC.
Um triângulo tem três mediatrizes de lados.
Na figura ao lado, as três mediatrizes são:
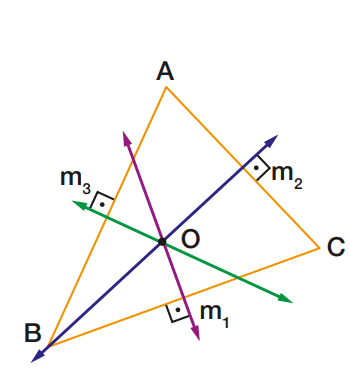
- m1 , mediatriz de BC;
- m2 , mediatriz de AC;
- m3, mediatriz de AB;
As três mediatrizes dos lados de um triângulo encontram-se num ponto chamado circuncentro do triângulo.
Na figura acima, O é o circuncentro do triângulo ABC.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Lista de exercício com solução de Pontos Notáveis do Triângulo
Exercício 01 – Relacione corretamente ao nome do ponto:
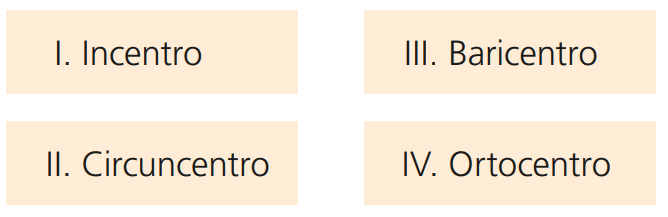
a) Ponto de encontro das medianas de um triângulo.
b) Ponto de encontro das bissetrizes de um triângulo.
c) Ponto de encontro das retas suportes das alturas de um triângulo.
d) Ponto de encontro das mediatrizes dos lados de um triângulo.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
a) III
b) I
c) IV
d) II
[/toggle]
Exercício 02 – Na figura abaixo, M é o ponto médio de AC.
Identifique:
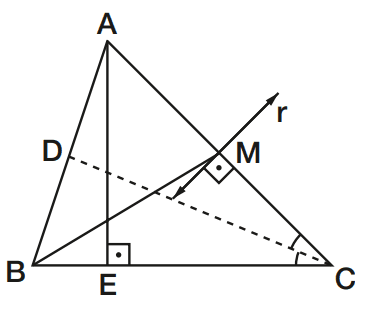
a) uma mediana;
b) uma bissetriz;
c) uma altura;
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
a) BM
b) CD
c) AE
[/toggle]
Exercício 03 – Nesta figura, AM é mediana. Calcule as medidas dos lados do triângulo.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 04 – No triângulo ABC abaixo, em que B mede 80° e C mede 60°, AS é bissetriz. Determine o ângulo x = BAS.
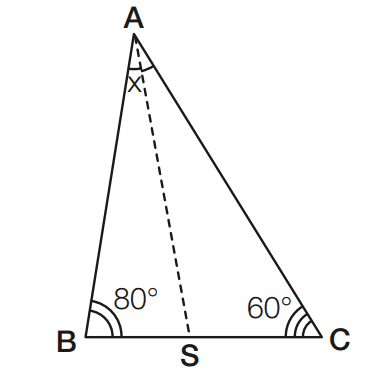
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
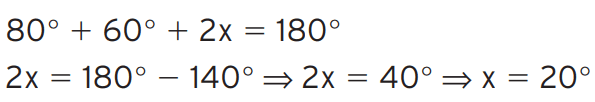
[/toggle]
Exercício 05 – No triângulo abaixo, retângulo em A (Â mede 90°), AH é altura. Determine x, y e z.
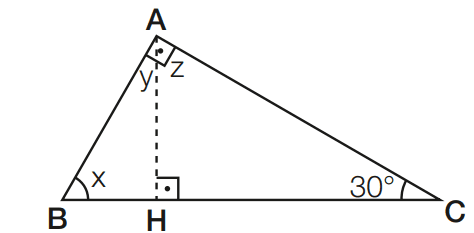
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
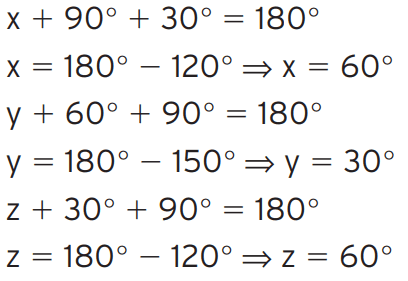
[/toggle]
Exercício 06 – Na figura, I é o incentro do triângulo ABC. Sabendo que BIC mede 8x e A mede x, determine x.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 07 – Quanto mede o ângulo formado pelas bissetrizes dos ângulos agudos de um triângulo retângulo?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
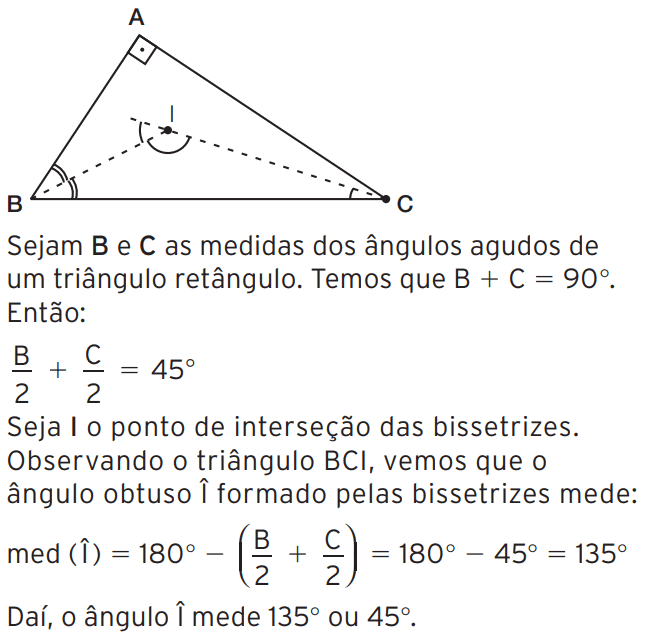
[/toggle]
Exercício 08 – No triângulo RST, RP é bissetriz. Determine x, y, z e t.
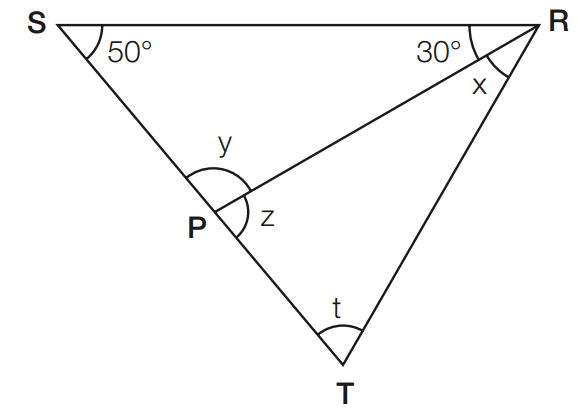
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
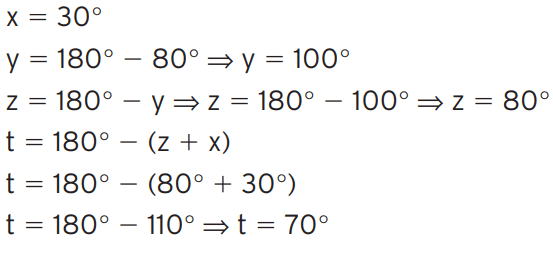
[/toggle]
Exercício 09 – Neste triângulo ABC, retângulo em A, AH é altura e AS é bissetriz. Calcule x, y e z.
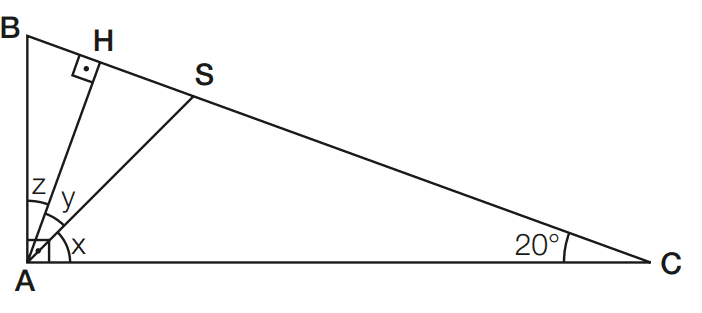
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
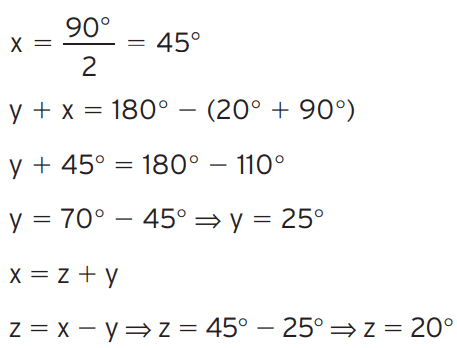
[/toggle]
Exercício 10 – No triângulo ABC abaixo, AH é altura e AS é bissetriz. Determine x.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
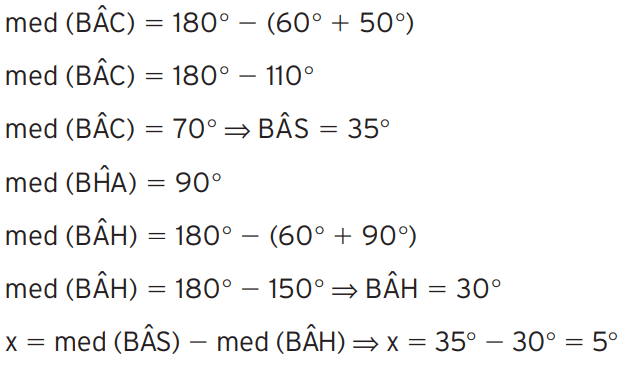
[/toggle]
Exercício 11 -No triângulo ABC, AS1 e BS2 são bissetrizes. Determine x.
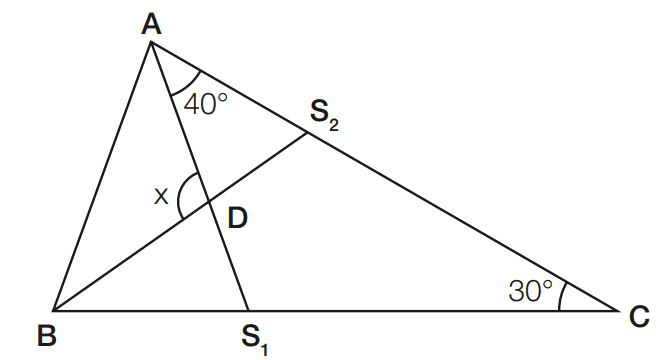
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
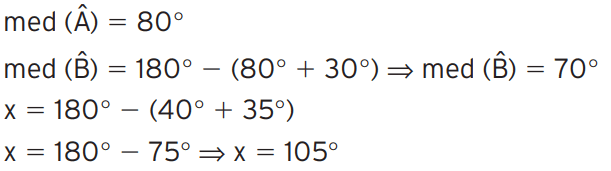
[/toggle]













