Prismas: Uma Análise Completa

Os prismas são sólidos geométricos formados por duas bases congruentes e paralelas ligadas por faces retangulares. Eles desempenham um papel importante em várias aplicações, desde a arquitetura até a física, e compreender suas propriedades geométricas é essencial para quem estuda matemática e suas aplicações. Neste artigo, exploraremos prismas com bases triangulares, quadradas e hexagonais, abordando conceitos como área da base, área lateral e volume.

Prismas com Base Triangular

Um prisma de base triangular possui duas bases que são triângulos congruentes. As faces laterais desse prisma são retângulos, e o número de faces laterais é sempre igual ao número de lados da base.

Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto
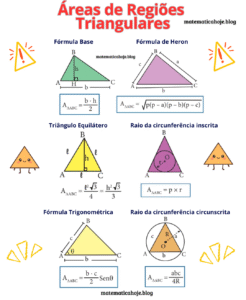
  • Área da Base: A área da base Ab de um prisma triangular é a área do triângulo que forma a base. Para um triângulo equilátero de lado a, área é dada por:
Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto
  • Área Lateral: A área lateral Al​ é a soma das áreas das faces retangulares. Se o prisma tem altura H e o lado do triângulo base são a, então a área lateral é dada por:
Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto
  • Volume: O volume V de um prisma triangular é dado pela área da base multiplicada pela altura H do prisma:
Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto

Área Total: A área total é a soma da área de todas as superfícies de um sólido geométrico, incluindo as áreas das bases e das faces laterais.

Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto

Prismas com Base Quadrada

Um prisma de base quadrada tem duas bases que são quadrados congruentes. As faces laterais são quatro retângulos iguais.

Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto
  • Área da Base: A área da base Ab de um prisma quadrado é simplesmente o quadrado do lado a da base:
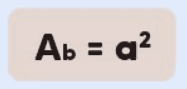
Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto
  • Área Lateral: A área lateral Al​ é a soma das áreas das quatro faces laterais. Com altura H do prisma, a área lateral é dada por:
Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto
  • Volume: O volume V de um prisma quadrado é dado pela área da base multiplicada pela altura H:
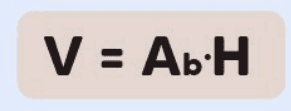
Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto

Área Total: A área total é a soma da área de todas as superfícies de um sólido geométrico, incluindo as áreas das bases e das faces laterais.

Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto

Prismas com Base Hexagonal

Um prisma de base hexagonal tem duas bases que são hexágonos regulares congruentes. Este prisma tem seis faces laterais, todas retangulares.

Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto
  • Área da Base: A área da base Ab​ de um prisma hexagonal pode ser calculada dividindo o hexágono em seis triângulos equiláteros. Se aaa é o lado do hexágono, a área da base é dada por:
Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto
  • Área Lateral: A área lateral Al​ é a soma das áreas das seis faces laterais. Com altura HHH do prisma, a área lateral é dada por:
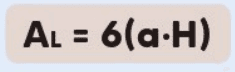
Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto
  • Volume: O volume V do prisma hexagonal é dado pela área da base multiplicada pela altura H:
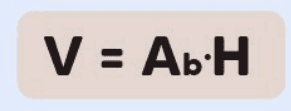
Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto

Área Total: A área total é a soma da área de todas as superfícies de um sólido geométrico, incluindo as áreas das bases e das faces laterais.

Tipos de prismas Prisma de base triangular Prisma triangular Prisma de base pentagonal Prisma quadrangular Prisma oblíquo Prisma de base hexagonal Prisma reto

Conclusão

Prismas são sólidos que aparecem frequentemente em aplicações práticas e teóricas. Seja com base triangular, quadrada ou hexagonal, os princípios para calcular área da base, área lateral e volume seguem padrões que facilitam o entendimento e a aplicação desses conceitos em problemas geométricos. Com essas fórmulas e explicações, estudantes e profissionais podem abordar problemas envolvendo prismas com confiança, utilizando o poder da geometria para resolver situações reais e teóricas.

Leia também

Prismas: Uma Análise Completa

O Cubo: Propriedades e Fórmulas Essenciais 

O Paralelepípedo: Propriedades e Fórmulas Essenciais

Pirâmides: Propriedades, Fórmulas e Aplicações 

Tetraedro Regular: Propriedades, Fórmulas e Aplicações

Tronco de Pirâmide: Propriedades, Fórmulas e Proporções 

Cilindro: Conceitos e Cálculos

Cone: Tudo o Que Você Precisa Saber

Esfera: Um Estudo Completo 

Poliedros: Estrutura, Teorema de Euler e Poliedros de Platão 

Relacionadas

O Paralelepípedo: Propriedades e Fórmulas Essenciais

O Cubo: Propriedades e Fórmulas Essenciais

Tronco de Pirâmide: Propriedades, Fórmulas e Proporções

"Artigo escrito por"

Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões Concurso

Mapas Mentais

Formulas Matemáticas

Instagram Facebook Youtube
Rolar para cima