Os quadriláteros, figuras geométricas com quatro lados, são elementos fundamentais no estudo da geometria plana. Eles aparecem em diversas formas e classificações, como o quadrado, o retângulo, o trapézio, o losango e o paralelogramo, cada um com suas propriedades únicas em relação aos lados, ângulos e diagonais.
Estudar quadriláteros é essencial para entender a relação entre forma e espaço, sendo aplicável tanto em situações do cotidiano quanto em problemas matemáticos complexos. Conhecer as fórmulas para cálculo de área, perímetro e outras características específicas de cada tipo de quadrilátero facilitará a resolução de questões geométricas.
Esta lista de exercícios é uma excelente oportunidade para praticar e solidificar seu conhecimento sobre quadriláteros, com desafios que exploram desde propriedades básicas até problemas mais elaborados, todos com soluções detalhadas para facilitar seu aprendizado.
01 – (Vunesp) A afirmação falsa é:
a) Todo quadrado é um losango.
b) Existem retângulos que não são losangos.
c) Todo paralelogramo é um quadrilátero.
d) Todo quadrado é um retângulo.
e) Um losango pode não ser um paralelogramo.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
02 – Na figura abaixo, D, E, F e G são os pontos médios de AB, AC, AE e DE, respectivamente.
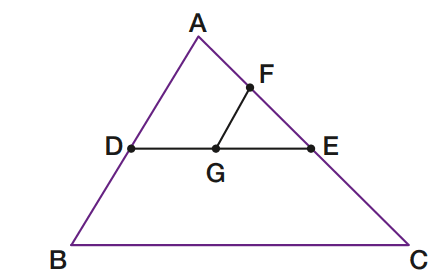
Se o perímetro do ∆EFG é 3,5 cm, então, o perímetro do ∆ABC é:
a) 7 cm
b) 10,5 cm
c) 14 cm
d) 17,5 cm
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
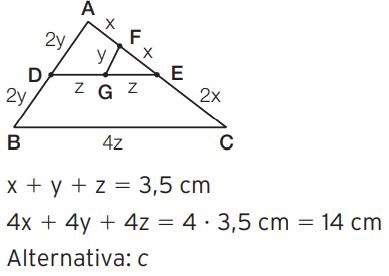
[/toggle]
03 – (ITASP) Considere um quadrilátero ABCD cujas diagonais AC e BD medem, respectivamente, 5 cm e 6 cm. Se R, S, T e U são os pontos médios dos lados do quadrilátero dado, então o perímetro do quadrilátero RSTU vale:
a) 22 cm
b) 5,5 cm
c) 8,5 cm
d) 11 cm
e) 13 cm
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
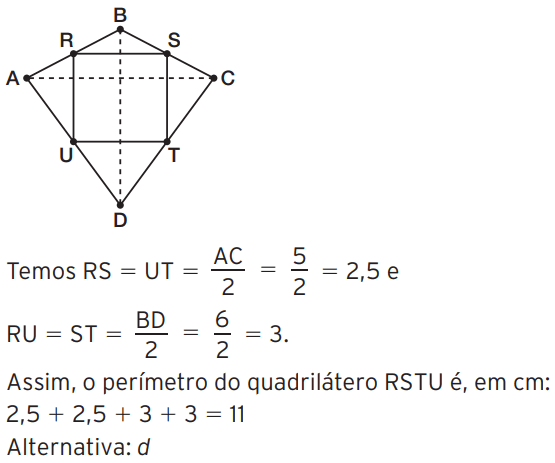
[/toggle]
04 – (FGVSP) A figura representa um trapézio isósceles ABCD, com AD = BC = 4 cm. M é o ponto médio de AD, e o ângulo BMˆ C é reto.
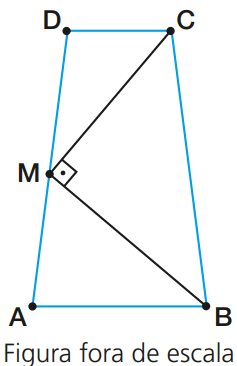
O perímetro do trapézio ABCD, em cm, é igual a:
a) 8.
b) 10.
c) 12.
d) 14.
e) 15.
(Sugestão do autor: trace a base média do trapézio; ela é mediana relativa à hipotenusa do triângulo retângulo.)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]


[/toggle]
05 – (UFMG) Na figura, ABCD é um quadrado e BCE é um triângulo equilátero.
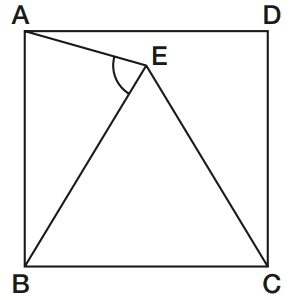
A medida do ângulo AEˆB, em graus, é:
a) 30
b) 49
c) 60
d) 75
e) 90
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
06 – (Obmep) O trapézio ABCD foi dobrado ao longo do segmento CE, paralelo ao lado AD, como na figura. Os triângulos EFG e BFH são equiláteros, ambos com lados de 4 cm de comprimento. Qual é o perímetro do trapézio?
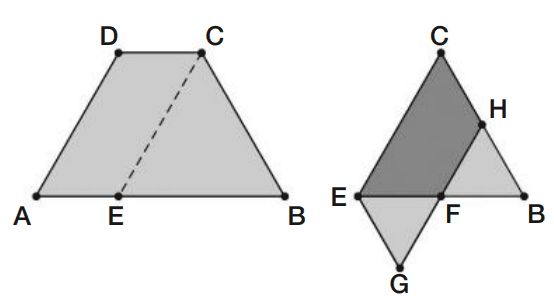
a) 16 cm
b) 18 cm
c) 20 cm
d) 24 cm
e) 32 cm
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
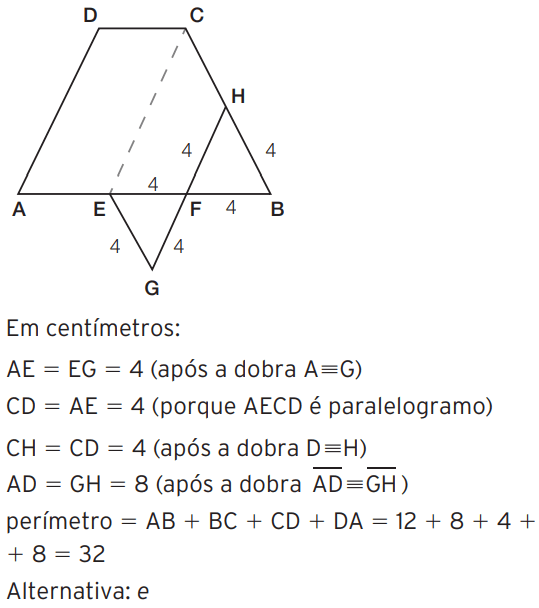
[/toggle]
07 – Sabendo que ABCD é um trapézio, P é ponto médio de AD e Q é ponto médio de BC, calcule x, y, z e o perímetro de ABCD.
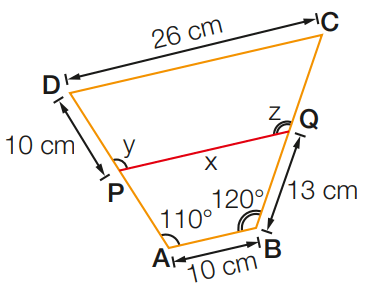
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
08 – Nas figuras, segmentos com marcas iguais são congruentes. Determine o valor de x em cada caso.
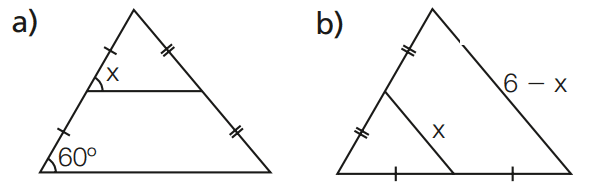
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
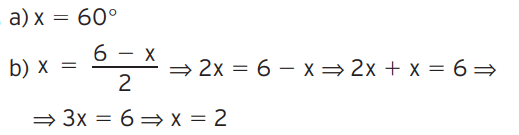
[/toggle]
09 – Em um triângulo ABC, os pontos M, N e R são os pontos médios dos lados AB, AC e BC, respectivamente. Se MN 5 7 cm, NR 5 4 cm e MR 5 8 cm, qual é o perímetro desse triângulo?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
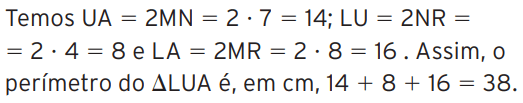
[/toggle]
10 – Sabendo que ABCD são trapézios isósceles de bases AB e CD, determine a medida de seus ângulos.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]