(CESPE / CEBRASPE 2024 – 2024 – Prefeitura de Joinville – SC – Professor Bilíngue)
Os 4 empregados de uma oficina de bicicleta trabalham, em média, 6 h por dia, 5 dias por semana, e consertam, em média, 30 bicicletas por semana.
Se o dono da oficina citada no texto CB1A2 aumentar o número de empregados para 9, mas diminuir o número de horas trabalhadas por dia para 4 h, sem alterar o número de dias trabalhados, o número médio de bicicletas consertadas por semana será
A) inferior a 43.
B) superior a 56.
C) superior a 44 e inferior a 47.
D) superior a 48 e inferior a 51.
E) superior a 52 e inferior a 55.
Para resolver o problema usando regra de três composta, vamos considerar as variáveis envolvidas: o número de empregados, o número de horas trabalhadas por dia e o número de bicicletas consertadas por semana.
Dados Iniciais
- Número de empregados: 4
- Horas trabalhadas por dia: 6 horas
- Dias trabalhados por semana: 5 dias
- Bicicletas consertadas por semana: 30 bicicletas
Nova Situação
- Número de empregados: 9
- Horas trabalhadas por dia: 4 horas
- Dias trabalhados por semana: 5 dias
- Bicicletas consertadas por semana: (x) bicicletas
Vamos resolver o problema aplicando a regra de três composta.
Montando a Regra de Três Composta
A relação entre as variáveis é direta. Se aumentamos o número de empregados ou o número de horas, a quantidade de bicicletas consertadas também aumenta, e vice-versa.
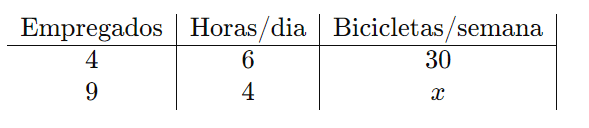
Agora, montamos a proporção considerando a relação direta entre as variáveis:
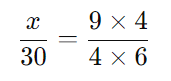
Passo 1: Simplificar a expressão
Primeiro, simplificamos a expressão na direita:
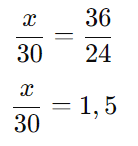
Passo 2: Resolver para x
Agora, isolamos x:
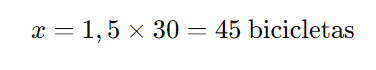
Resposta
Portanto, o número médio de bicicletas consertadas por semana na nova situação será 45 bicicletas, o que corresponde à Alternativa C: superior a 44 e inferior a 47.

























