Vamos considerar um triângulo equilátero ABC e chamar de AP e BQ duas medianas.
Como AB ≡ AC, esse triângulo é isósceles de base BC; logo:
- B ≡ C;
- AP é mediana, altura e bissetriz.
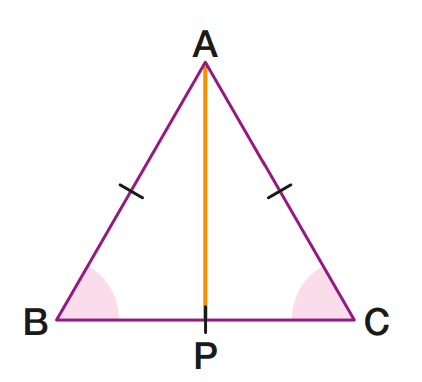
Como AB ≡ BC, esse triângulo também é isósceles de base AC; logo:
- A ≡ C;
- BQ é mediana, altura e bissetriz.
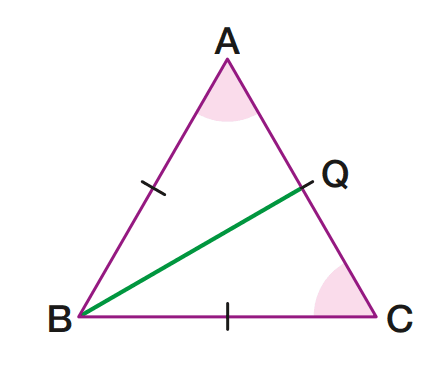
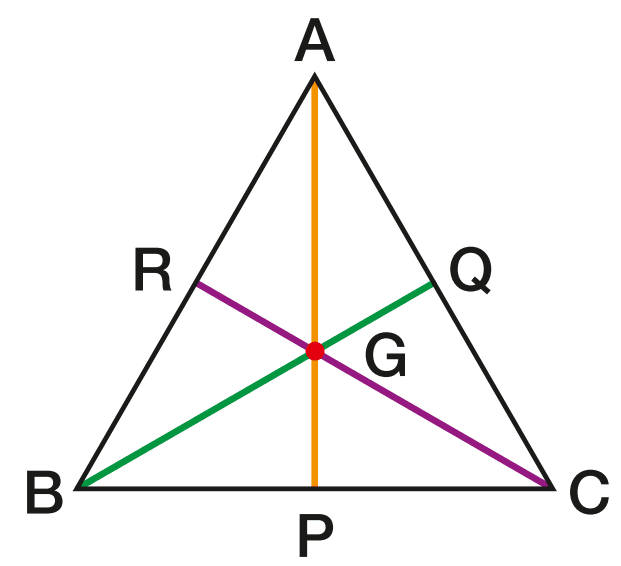
Em resumo, se o triângulo ABC é equilátero e os pontos médios de seus lados são P, Q e R, então:
- A ≡ B ≡ C;
- AP, BQ e CR são medianas, alturas e bissetrizes;
- G é baricentro, ortocentro e incentro
Todo triângulo equilátero é equiângulo.
Também vale a recíproca:
Todo triângulo equiângulo é equilátero
Lista de Exercício com Solução de Triângulo Equilátero
Exercício 01 – Quanto medem os ângulos de um triângulo equilátero?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Os três ângulos têm medidas iguais. Cada um mede: 180/3 = 60°
Mede 60 graus
[/toggle]
Exercício 02 – Nas figuras abaixo, segmentos com marcas iguais são congruentes. Determine x em cada item.
a)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
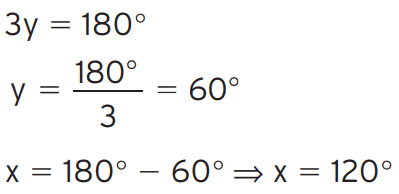
[/toggle]
b)
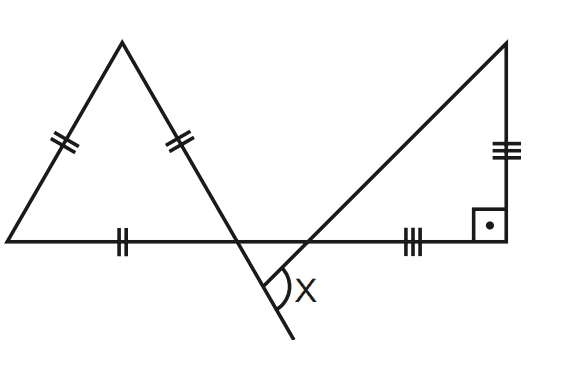
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
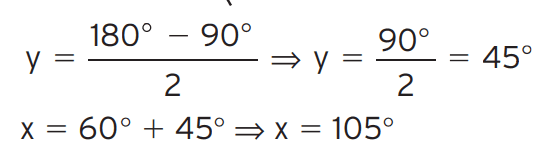
[/toggle]
Exercício 03 – Na figura, o triângulo ABC é equilátero, e o triângulo CDB é isósceles. Calcule as medidas dos ângulos BCD e ABD.
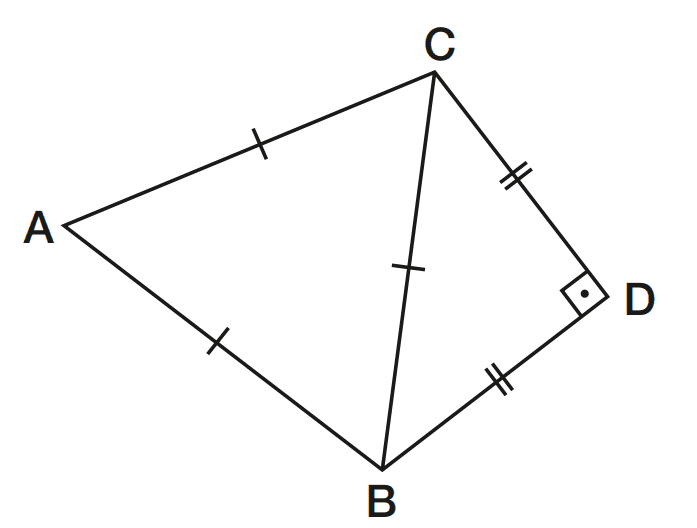
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Se o triângulo ABC é equilátero, então a medida de cada ângulo interno vale 60°
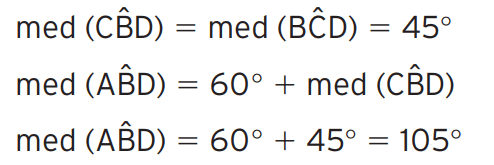
[/toggle]
Exercício 04 – Num triângulo isósceles ABC de base BC, um dos ângulos da base mede 40°. Determine o ângulo obtuso formado pelas bissetrizes BP e CR.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
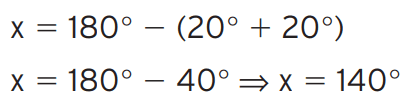
[/toggle]
Exercício 05 – O triângulo ABC é isósceles de base BC, e BP é bissetriz. Calcule x, y e z.
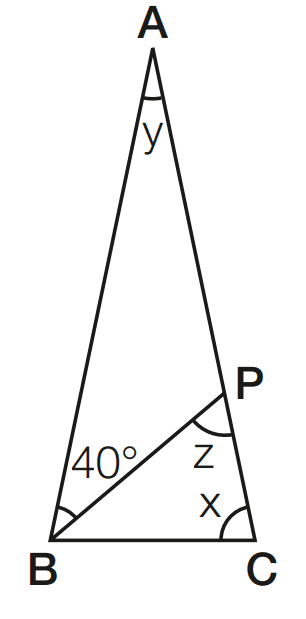
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
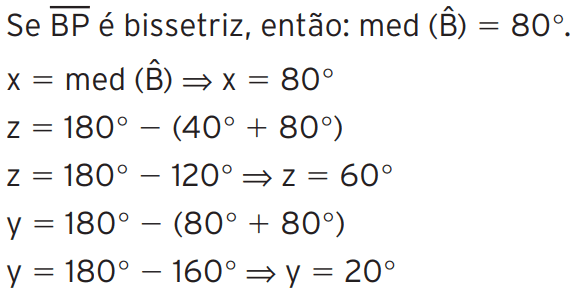
[/toggle]
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.













