A circunferência é uma das formas geométricas mais fundamentais e frequentemente encontradas em nosso cotidiano, desde a roda de um carro até a base de uma xícara. Neste artigo, exploraremos os principais conceitos relacionados à circunferência, como tangente, corda, raio e diâmetro, além de discutirmos como calcular a área e o comprimento dessa forma geométrica.
O que é uma Circunferência?
Uma circunferência é o conjunto de todos os pontos em um plano que estão a uma distância fixa, chamada de raio, de um ponto central. A linha que define a circunferência é a própria circunferência, enquanto o espaço interno é chamado de círculo.
Conceitos Fundamentais
1. Tangente
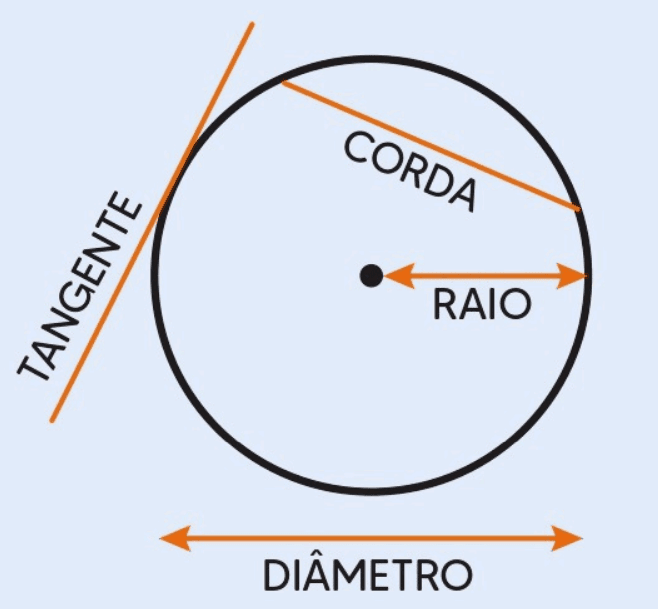
A tangente a uma circunferência é uma linha reta que toca a circunferência em exatamente um ponto. Esse ponto é chamado de ponto de tangência. Uma propriedade importante da tangente é que ela é sempre perpendicular ao raio da circunferência no ponto de tangência.
Propriedade: Se uma reta é tangente a uma circunferência, então a distância entre o centro da circunferência e a reta é igual ao raio da circunferência.
2. Corda
Uma corda é um segmento de reta cujas extremidades estão sobre a circunferência. Uma corda divide a circunferência em duas partes, chamadas de arcos. Se a corda passa pelo centro da circunferência, ela se torna um diâmetro.
Propriedade: A maior corda de uma circunferência é o diâmetro, que é igual ao dobro do raio.
3. Raio
O raio é a distância fixa entre o centro da circunferência e qualquer ponto sobre a circunferência. Todos os raios de uma circunferência têm o mesmo comprimento.
4. Diâmetro
O diâmetro é uma corda especial que passa pelo centro da circunferência, sendo, portanto, o maior segmento que pode ser desenhado dentro de uma circunferência. O diâmetro é o dobro do raio.
Propriedade: Todos os raios de uma mesma circunferência são congruentes.
Fórmula:
Diâmetro=2×Raio
Cálculos Essenciais
1. Área da Circunferência
A área de um círculo, que é a região interna à circunferência, pode ser calculada com a seguinte fórmula:

onde r é o raio da circunferência e π(pi) é uma constante matemática aproximadamente igual a 3,14159.
2. Comprimento da Circunferência
O comprimento da circunferência é a distância ao redor da borda da circunferência. Ele pode ser calculado com a seguinte fórmula:
Comprimento=2×π×r
ou, alternativamente, usando o diâmetro:
Comprimento= π×Diâmetro
Aplicações e Importância
A circunferência é uma forma geométrica central em várias disciplinas e aplicações práticas:
- Engenharia: O cálculo de circunferências é essencial no design de engrenagens, rodas e tubos.
- Arquitetura: Circunferências e círculos são frequentemente usados no design de cúpulas e arcos.
- Ciências Naturais: Muitos fenômenos naturais, como as órbitas planetárias, são descritos por circunferências ou formas circulares.
Exemplos Práticos
- Exemplo 1: Calcular a área de uma circunferência com raio de 5 cm.

Exemplo 2: Calcular o comprimento de uma circunferência com diâmetro de 10 cm.
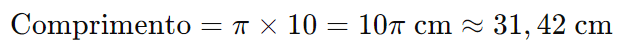

Conclusão
Compreender os conceitos de tangente, corda, raio e diâmetro, bem como saber calcular a área e o comprimento da circunferência, é fundamental não só na geometria, mas em muitas áreas práticas da ciência e da engenharia. A circunferência, com suas propriedades e cálculos, continua sendo uma das formas geométricas mais estudadas e aplicadas em diversos campos do conhecimento.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes










