Os triângulos são uma das figuras geométricas mais fundamentais e versáteis na matemática e na vida cotidiana. Eles podem ser encontrados em diversas formas e tamanhos, e sua compreensão é crucial para o estudo de geometria e trigonometria. Neste artigo, vamos explorar os triângulos em profundidade, classificando-os de acordo com seus lados e ângulos, e destacando suas propriedades únicas.
1. Classificação dos Triângulos em Função dos Lados
Os triângulos podem ser classificados com base no comprimento de seus lados. Esta classificação nos ajuda a entender as propriedades específicas de cada tipo de triângulo.
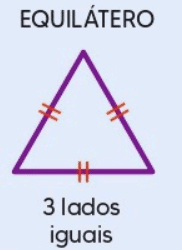
1.1 Triângulo Equilátero
Um triângulo equilátero é aquele em que todos os três lados têm o mesmo comprimento. Além disso, todos os ângulos internos de um triângulo equilátero são iguais e medem 60 graus cada. Devido à sua simetria, o triângulo equilátero possui várias propriedades notáveis, como a congruência de suas medianas, alturas e bissetrizes.
Propriedades principais:
- Todos os ângulos são iguais (60 graus).
- Todos os lados são congruentes.
- As medianas, alturas e bissetrizes são iguais e se encontram no mesmo ponto.
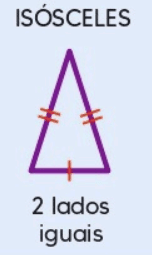
1.2 Triângulo Isósceles
Um triângulo isósceles possui pelo menos dois lados de comprimentos iguais. Os ângulos opostos a esses lados iguais também são iguais. Esta característica proporciona várias propriedades úteis, como a capacidade de determinar a medida de um ângulo se conhecemos a medida dos outros.
Propriedades principais:
- Dois lados são congruentes.
- Os ângulos opostos a esses lados iguais também são iguais.
- A altura que é traçada a partir do vértice do ângulo formado pelos dois lados iguais divide o triângulo em dois triângulos retângulos congruentes.
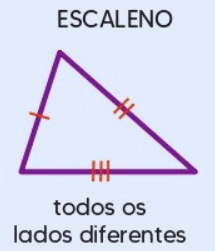
1.3 Triângulo Escaleno
Um triângulo escaleno é aquele em que todos os lados têm comprimentos diferentes. Como resultado, todos os ângulos internos também são diferentes. Os triângulos escaleno são bastante diversos em forma e podem ter qualquer configuração de ângulos e lados.
Propriedades principais:
- Todos os lados têm comprimentos diferentes.
- Todos os ângulos são diferentes.
- Não há simetria em termos de lados ou ângulos.
2. Classificação dos Triângulos em Função dos Ângulos
Os triângulos também podem ser classificados com base na medida de seus ângulos internos. Esta classificação é útil para entender a forma e o comportamento dos triângulos.
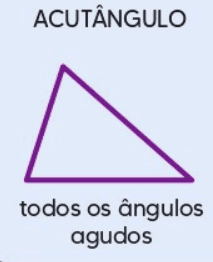
2.1 Triângulo Acutângulo
Um triângulo acutângulo é aquele em que todos os três ângulos internos são agudos, ou seja, cada ângulo mede menos de 90 graus. Este tipo de triângulo é geralmente mais “apertado” e não possui ângulos maiores.
Propriedades principais:
- Todos os ângulos são menores de 90 graus.
- Pode ser equilátero (se todos os ângulos são exatamente 60 graus) ou isósceles (se dois ângulos são iguais e menores de 90 graus).
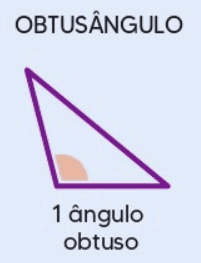
2.2 Triângulo Obtusângulo
Um triângulo obtusângulo é aquele que possui um ângulo obtuso, ou seja, um ângulo maior que 90 graus. Os outros dois ângulos devem ser agudos para que a soma dos ângulos internos seja igual a 180 graus.
Propriedades principais:
- Um dos ângulos é maior de 90 graus (obtuso).
- Os outros dois ângulos são menores de 90 graus.
- O lado oposto ao ângulo obtuso é o maior lado do triângulo.
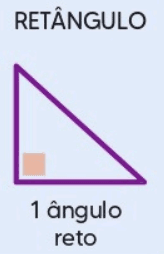
2.3 Triângulo Retângulo
Um triângulo retângulo possui um ângulo reto, que mede exatamente 90 graus. O lado oposto ao ângulo reto é chamado de hipotenusa e é o lado mais longo do triângulo. Os outros dois lados são chamados de catetos.
Propriedades principais:
- Um dos ângulos é exatamente 90 graus.
- A soma dos quadrados dos comprimentos dos catetos é igual ao quadrado do comprimento da hipotenusa, conforme o Teorema de Pitágoras.
- Pode ser classificado ainda como acutângulo ou obtusângulo, dependendo da medida dos outros dois ângulos.
Resumo: Tipos de Triângulos e Suas Propriedades
Os triângulos são figuras geométricas essenciais com diversas formas e propriedades. Eles podem ser classificados de acordo com seus lados e ângulos.
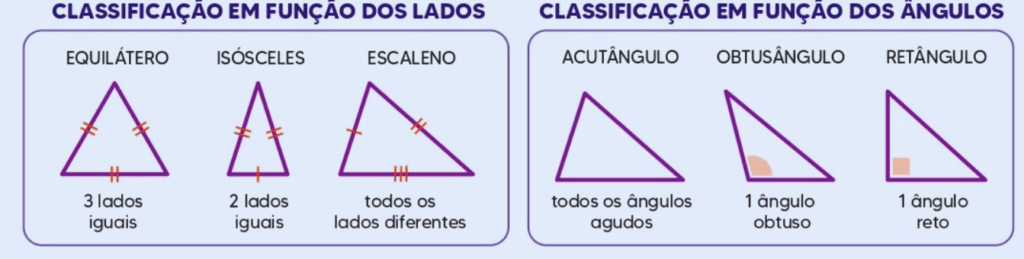
Classificação pelos Lados
- Equilátero: Todos os três lados e ângulos são iguais (60 graus cada).
- Isósceles: Dois lados e ângulos são iguais. A altura a partir do vértice divide o triângulo em dois triângulos retângulos congruentes.
- Escaleno: Todos os lados e ângulos são diferentes.
Classificação pelos Ângulos
- Acutângulo: Todos os ângulos são agudos (menores que 90 graus).
- Obtusângulo: Um ângulo é obtuso (maior que 90 graus); os outros dois são agudos.
- Retângulo: Um ângulo é reto (90 graus). A hipotenusa é o lado mais longo e a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa (Teorema de Pitágoras).
Conhecer essas classificações ajuda a entender melhor as propriedades e aplicações dos triângulos na matemática e no cotidiano.
Conclusão
Os triângulos são figuras geométricas fascinantes e versáteis que vêm em várias formas e tamanhos. A classificação dos triângulos com base em seus lados e ângulos nos fornece uma compreensão mais profunda de suas propriedades e aplicações. Seja em projetos de engenharia, arte ou arquitetura, a compreensão dos triângulos é essencial para resolver problemas e criar soluções inovadoras.
Ao estudar triângulos, é importante praticar a identificação e aplicação das propriedades discutidas. Isso não apenas ajudará a compreender melhor a geometria, mas também a desenvolver habilidades críticas de resolução de problemas. Portanto, continue explorando e experimentando com triângulos e descubra as inúmeras maneiras em que eles podem ser usados e aplicados!
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes