Enunciado:
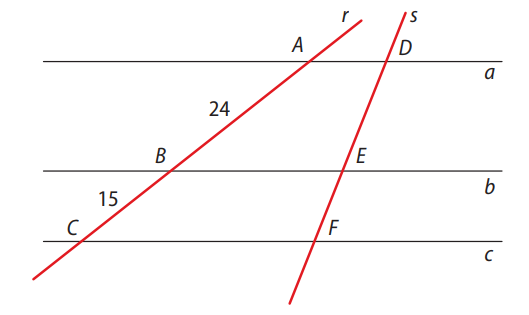
Observe a figura a seguir, em que as retas \( a, b \) e \( c \) são paralelas, e as medidas estão em centímetros. Deseja-se determinar as medidas dos segmentos \( \overline{DE} \) e \( \overline{EF} \).
a) A partir das informações dadas, é possível resolver o problema?
b) Se for possível, resolva o problema. Se não for possível, indique quais informações estão faltando para que as medidas possam ser encontradas.
👇 Ver análise e justificativa
Resposta da letra (a): Não.
Justificativa:
O Teorema de Tales exige que as proporções sejam feitas entre segmentos correspondentes de duas transversais que cruzam um feixe de retas paralelas. Na figura, temos as retas \( a \), \( b \) e \( c \) paralelas, mas as transversais \( r \) e \( s \) não têm todos os seus segmentos medidos.
Apenas temos os comprimentos de \( \overline{AB} = 24\,\text{cm} \) e \( \overline{BC} = 15\,\text{cm} \), mas falta o valor total de \( \overline{AC} \), e principalmente, não temos nenhuma medida nos segmentos da outra transversal (\( \overline{DE}, \overline{EF} \)) que permita montar uma proporção.
Resposta da letra (b):
Para que o problema possa ser resolvido, seria necessário conhecer, por exemplo:
- O comprimento de \( \overline{DF} \) na transversal \( s \);
- Ou o valor de \( \overline{DE} \) ou \( \overline{EF} \) separadamente;
- Ou ainda a razão entre os lados da transversal \( s \) que tornaria possível aplicar o Teorema de Tales.
Conclusão: Com os dados apresentados, não é possível resolver o problema.
🔗 Material complementar gratuito
📌 Quer praticar mais?
Confira uma seleção incrível com 8 exercícios resolvidos sobre Teorema de Tales e Proporcionalidade, todos com figuras, explicações detalhadas e solução passo a passo com botão de abre/fecha:













