📘 Questão 30 – Geometria – Triplas Pitagóricas e Padrões Quadrados
(UERJ) Segundo historiadores da matemática, a análise de padrões como os ilustrados a seguir possibilitou a descoberta das triplas pitagóricas.
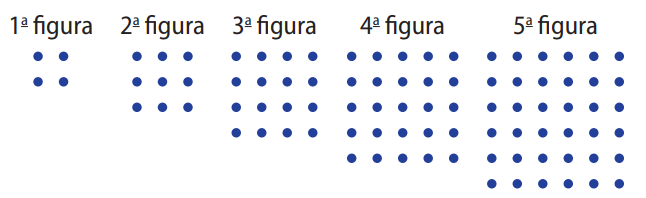
Observe que os números inteiros \(3^2\), \(4^2\) e \(5^2\), representados pelas 2ª, 3ª e 4ª figuras, satisfazem ao Teorema de Pitágoras. Dessa forma, \((3,\ 4,\ 5)\) é uma tripla pitagórica.
Os quadrados representados pelas 4ª, 11ª e \(n\)-ésima figuras determinam outra tripla pitagórica. Determine o valor de \(n\):
- a) 10
- b) 12
- c) 14
- d) 16
👀 Ver solução passo a passo
1. Análise do padrão:
Cada figura representa um quadrado de ordem crescente:
- 1ª figura → \(1^2 = 1\)
- 2ª figura → \(2^2 = 4\)
- 3ª figura → \(3^2 = 9\)
- 4ª figura → \(4^2 = 16\)
- …
A 11ª figura representa:
\[ 11^2 = 121 \]Desejamos encontrar o valor de \(n\) tal que as figuras 4ª, 11ª e \(n\) formem uma tripla pitagórica, ou seja:
\[ 4^2 + 11^2 = n^2 \]2. Aplicando o Teorema de Pitágoras:
\[ 16 + 121 = n^2 \] \[ 137 = n^2 \] \[ n = \sqrt{137} \approx 11{,}7 \]Como os quadrados são numerados com base em números inteiros, e não existe figura “11,7”, a figura mais próxima que representa esse valor é:
\[ n = 12 \]✅ Resposta correta: Letra b) 12
🎯 Continue aprendendo com nossos materiais exclusivos:
📘 Lista completa disponível:
Veja todas as 8 questões resolvidas sobre Trigonometria no Triângulo Retângulo e Teorema de Pitágoras, com explicações visuais, passo a passo e recursos extras para revisar e aprender com clareza.
👉 Acessar a Lista Completa📄 Leia também:
Entenda de forma clara e prática as 🔺 Relações Métricas no Triângulo Retângulo com explicações passo a passo, figuras e aplicações diretas em exercícios. Ideal para quem está estudando trigonometria, geometria ou se preparando para concursos!
👉 Acessar o Artigo Completo