📘 Questão 32 – Teorema de Pitágoras – Triângulo Retângulo
(Unichristus) Um drone, em um ponto \( A \), foi utilizado para localizar focos de incêndio na mata. Este drone está a uma altura \( H \) do solo e detecta dois focos nos pontos \( B \) e \( C \), como mostrado na figura:
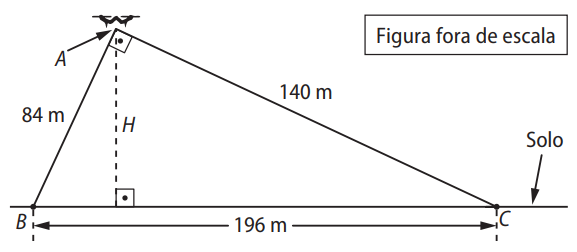
Sabendo que:
- \( AB = 84\ \text{m} \)
- \( AC = 140\ \text{m} \)
- \( BC = 196\ \text{m} \)
E que o triângulo \( ABC \) é retângulo em \( A \), determine a altura \( H \) do drone em relação ao solo.
- a) 45 m
- b) 50 m
- c) 55 m
- d) 60 m
- e) 65 m
👀 Ver solução passo a passo
O triângulo \( ABC \) é retângulo em \( A \), então aplicamos o Teorema de Pitágoras:
\( BC^2 = AB^2 + AC^2 \)
\[ 196^2 = 84^2 + 140^2 \] \[ 38416 = 7056 + 19600 \] \[ 38416 = 26656 \quad \text{(não confere!)} \]Na verdade, a hipotenusa deve ser o lado oposto ao ângulo reto. Como o ângulo reto é em \( A \), o lado oposto é \( BC = 196 \).
Para encontrar \( H \), usamos o triângulo retângulo \( ABC \), com catetos \( H \) e \( x \), e hipotenusa \( AC = 140 \).
\[ H^2 + x^2 = 140^2 \]Sabemos que:
\[ x = BC – AB = 196 – 84 = 112\ \text{m} \]\[ H^2 = 140^2 – 112^2 \] \[ H^2 = 19600 – 12544 = 7056 \] \[ H = \sqrt{7056} = \boxed{60\ \text{m}} \]✅ Resposta correta: Letra d) 60 m
🎓 Estude mais com nossos materiais gratuitos:
📘 Lista completa disponível:
Veja todas as 8 questões resolvidas sobre Trigonometria no Triângulo Retângulo e Teorema de Pitágoras, com explicações visuais, passo a passo e recursos extras para revisar e aprender com clareza.
👉 Acessar a Lista Completa📄 Leia também:
Entenda de forma clara e prática as 🔺 Relações Métricas no Triângulo Retângulo com explicações passo a passo, figuras e aplicações diretas em exercícios. Ideal para quem está estudando trigonometria, geometria ou se preparando para concursos!
👉 Acessar o Artigo Completo