No estudo da trigonometria, as razões trigonométricas são fundamentais para compreender a relação entre os lados e os ângulos de um triângulo retângulo. Neste artigo, vamos explorar o conceito de seno, cosseno e tangente de um ângulo agudo, além de apresentar suas propriedades, fórmulas e demonstrações visuais.
📐 Aplicações no Cotidiano: Inclinação de Rampas
Antes de aprofundarmos nas definições matemáticas, observe o exemplo de uma rampa de acesso. Em projetos arquitetônicos, é comum utilizar triângulos retângulos para calcular a inclinação da rampa, o comprimento necessário e o ângulo formado com o chão.
📌 Imagem 1: Triângulo retângulo formado pela rampa, altura e projeção no solo.
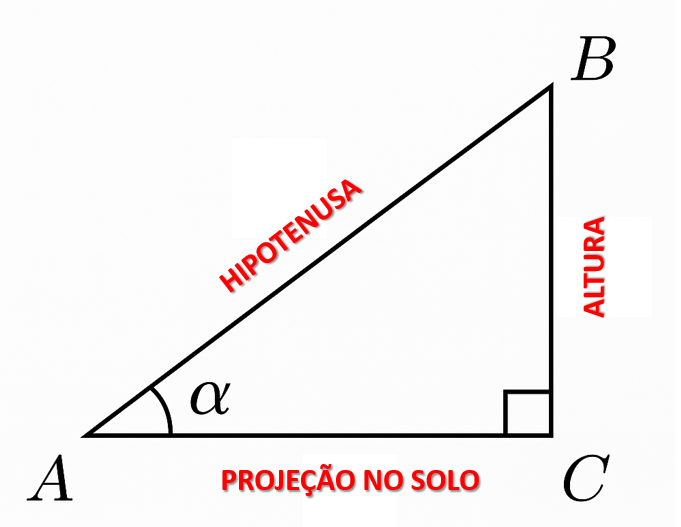
Com base no triângulo \( \triangle ABC \):
- k1 = \( \dfrac{\text{altura}}{\text{hipotenusa}} \Rightarrow sen{\alpha} \)
- k2 = \( \dfrac{\text{projeção no solo}}{\text{hipotenusa}} \Rightarrow \cos{\alpha} \)
- k3 = \( \dfrac{\text{altura}}{\text{projeção no solo}} \Rightarrow \tan{\alpha} \)
📌 Definições das Razões Trigonométricas
🔹 Seno (sen)
O seno de um ângulo agudo \( \alpha \) é definido como:
🔹 Cosseno (cos)
O cosseno de um ângulo agudo \( \alpha \) é:
🔹 Tangente (tg)
A tangente de um ângulo agudo \( \alpha \) é:
📏 Relações Entre as Razões Trigonométricas
🔸 1ª Relação – Fundamental da Trigonometria
Para qualquer ângulo agudo \( \alpha \):
🔸 2ª Relação – Complementares
O seno de um ângulo é igual ao cosseno do seu complementar:
🔸 3ª Relação – Tangente com Seno e Cosseno
A tangente de \( \alpha \) também pode ser expressa como:
📘 Conclusão
As razões trigonométricas são ferramentas essenciais na matemática e possuem ampla aplicação em problemas práticos, como arquitetura, física e engenharia. Dominar seno, cosseno e tangente é o primeiro passo para avançar em tópicos como funções trigonométricas, gráficos e equações.
📚 Veja também:
🔗 Baixe também nossos 10 eBooks gratuitos de Matemática e acesse nossos mapas mentais de matemática para revisar com clareza!
Questão 1 – Inclinação de Rampas
Enunciado:
Observe a representação de duas rampas com ângulos de inclinação diferentes. É possível determinar qual das duas rampas tem maior inclinação? Explique.
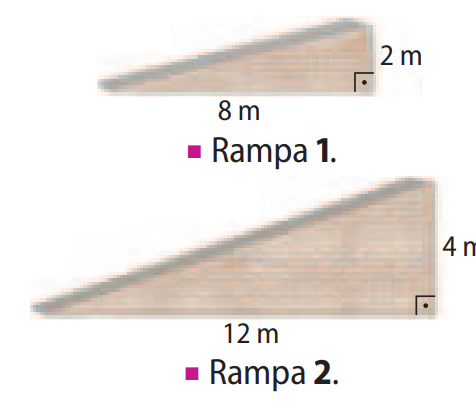
Solução:
Sim, podemos determinar qual das duas rampas tem maior inclinação calculando a razão entre a altura e o comprimento horizontal, que é equivalente à tangente do ângulo de inclinação.
Sendo \( \alpha \) e \( \beta \) os ângulos de inclinação das rampas 1 e 2, respectivamente, temos:
\[ \tan \alpha = \frac{2}{8} = \frac{1}{4} \] \[ \tan \beta = \frac{4}{12} = \frac{1}{3} \]
Agora, comparamos as duas razões:
\[ \frac{1}{4} = 0,25 < \frac{1}{3} \approx 0,33 \]
Isso significa que, para um mesmo comprimento horizontal (12 m), a rampa 1 corresponderia a uma altura de 3 m, enquanto a rampa 2 corresponde a uma altura de 4 m.
Conclusão: A rampa 2 tem maior inclinação do que a rampa 1.
📌 Recursos complementares:
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na AmazonQuestão 2 – Medição da Altura de uma Torre
Enunciado:
Para medir a altura de uma torre, uma topógrafa se situa no ponto A, a 70 m da base da torre. Em seguida, com o teodolito, mira o ponto mais alto da torre e verifica que o ângulo de observação com a horizontal é de \(32^\circ\). Sabendo que a distância do teodolito ao chão é desprezível, calcule a altura da torre. Considere \(\tan 32^\circ = 0{,}625\).
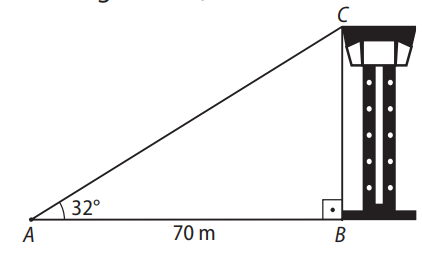
Solução:
Vamos representar a situação no triângulo \( \triangle ABC \), onde:
- \(AB = 70 \, \text{m}\) é a distância da topógrafa à base da torre;
- \(BC\) é a altura da torre que queremos determinar;
- O ângulo em \(A\) é \(32^\circ\).
Sabemos que:
\[ \tan 32^\circ = \frac{BC}{AB} \]
Substituindo os valores fornecidos:
\[ 0{,}625 = \frac{BC}{70} \]
Multiplicando cruzado:
\[ BC = 70 \cdot 0{,}625 = 43{,}75 \, \text{m} \]
Portanto, a altura da torre é \( BC = 43{,}75 \, \text{m} \).
📌 Recursos complementares:
Confira Nossa Lista Completa
Questão 3 – Cálculo da Tangente
Enunciado:
Sabendo que \( \alpha \) é um ângulo agudo de um triângulo retângulo \( ABC \) e que \( \cos (90^\circ – \alpha) = \dfrac{1}{3} \), calcule o valor de \( \tan \alpha \).
Solução:
Sabemos que:
\[ sen \alpha = \cos (90^\circ – \alpha) = \frac{1}{3} \]
Pela relação fundamental da trigonometria:
\[ sen^2 \alpha + \cos^2 \alpha = 1 \]
Substituindo \( sen \alpha = \frac{1}{3} \):
\[ \left( \frac{1}{3} \right)^2 + \cos^2 \alpha = 1 \quad \Rightarrow \quad \frac{1}{9} + \cos^2 \alpha = 1 \quad \Rightarrow \quad \cos^2 \alpha = \frac{8}{9} \]
\[ \cos \alpha = \frac{2 \sqrt{2}}{3} \]
Agora, usando a relação \( \tan \alpha = \frac{sen \alpha}{\cos \alpha} \):
\[ \tan \alpha = \frac{\frac{1}{3}}{\frac{2 \sqrt{2}}{3}} = \frac{1}{2 \sqrt{2}} = \frac{\sqrt{2}}{4} \]
Portanto, \( \tan \alpha = \frac{\sqrt{2}}{4} \).
📌 Recursos complementares:
Confira Nossa Lista Completa
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon























