Domine os principais temas de Matemática com esta seleção de 11 questões comentadas, todas com imagens, esquemas e soluções passo a passo. Ideal para quem está se preparando para vestibulares, concursos ou olimpíadas. Aprenda de forma clara com aplicação de Teorema de Pitágoras, Semelhança de Triângulos, Porcentagem, Geometria Plana, Funções e muito mais. Ao final de cada questão, indicamos materiais de apoio como mapas mentais e eBooks gratuitos.
Questão 1
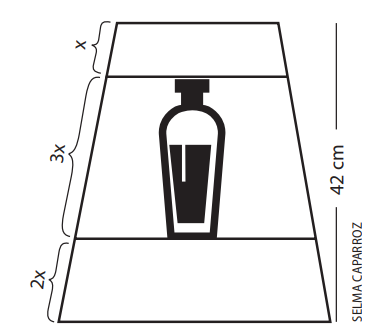
A figura acima mostra um armário de banheiro que tem o formato de um trapézio. A altura total do armário é de 42 cm e ele está dividido em três compartimentos. As medidas de um dos lados de cada compartimento estão indicadas na figura.
Desprezando a espessura das divisórias, podemos afirmar que no compartimento do meio podemos colocar um produto com altura máxima de:
Alternativas:
- a) 10 cm
- b) 14 cm
- c) 18 cm
- d) 21 cm
- e) 25 cm
Solução Passo a Passo:
Vamos chamar a altura do compartimento superior de \( x \). Segundo a figura, o compartimento do meio mede \( 3x \) e o inferior mede \( 2x \).
Somando todas as partes:
\[ x + 3x + 2x = 6x \]
Como a altura total do armário é 42 cm:
\[ 6x = 42 \] \[ x = 7 \]
Com isso, a altura do compartimento do meio é:
\[ 3x = 3 \cdot 7 = \boxed{21\,\text{cm}} \]
Resposta correta: letra d.
📌 Aproveite também:
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na AmazonQuestão 2
(Unemat-MT) A sombra de uma pessoa que tem 1,80 m de altura mede 60 cm. No momento, a seu lado, a sombra projetada de um poste mede 2,00 m. Se mais tarde, a sombra do poste diminuir 50 cm, a sombra da pessoa passará a medir:
Alternativas:
- a) 30 cm
- b) 45 cm
- c) 48 cm
- d) 36 cm
- e) 25 cm
Solução Passo a Passo:
Vamos usar a semelhança dos triângulos formados pela pessoa e pelo poste com suas respectivas sombras.
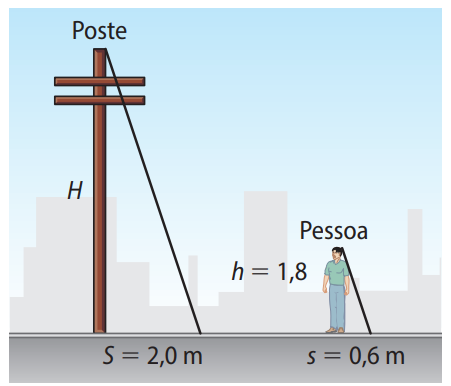
Altura da pessoa: \( h = 1{,}8 \, \text{m} \)
Sombra da pessoa: \( s = 0{,}6 \, \text{m} \)
Sombra do poste: \( S = 2{,}0 \, \text{m} \)
Vamos determinar a altura do poste \( H \), usando a proporção:
\[ \frac{H}{S} = \frac{h}{s} \] \[ \frac{H}{2{,}0} = \frac{1{,}8}{0{,}6} \] \[ \frac{H}{2{,}0} = 3 \Rightarrow H = 3 \cdot 2{,}0 = 6{,}0 \, \text{m} \]
Agora que sabemos que o poste tem 6,0 m de altura, vamos calcular o novo comprimento da sombra da pessoa quando a sombra do poste diminui 50 cm:
Nova sombra do poste: \( S’ = 2{,}0 – 0{,}5 = 1{,}5 \, \text{m} \)
Usamos novamente a razão da semelhança:
\[ \frac{H}{S’} = \frac{h}{s’} \] \[ \frac{6{,}0}{1{,}5} = \frac{1{,}8}{s’} \] \[ 4 = \frac{1{,}8}{s’} \Rightarrow s’ = \frac{1{,}8}{4} = 0{,}45 \, \text{m} = \boxed{45\,\text{cm}} \]
Resposta correta: letra b.
📌 Aproveite também:
📏 Estude Mais: Relações Métricas no Triângulo Retângulo
Aprofunde seu conhecimento com o artigo completo que explica passo a passo como aplicar as relações métricas no triângulo retângulo. Ideal para quem deseja dominar esse tema com teoria e exemplos visuais!
🔗 Acessar o artigo agora📏 Estude Mais: Relações Métricas no Triângulo Retângulo
Aprofunde seu conhecimento com o artigo completo que explica passo a passo como aplicar as relações métricas no triângulo retângulo. Ideal para quem deseja dominar esse tema com teoria e exemplos visuais!
🔗 Acessar o artigo agoraQuestão 3
(IFSC) Para determinar a altura de um poste, Ana utilizou o seguinte artifício, com o auxílio de uma colega: mediu sua sombra e a do poste, obtendo 2,4 m e 3,7 m, respectivamente. Se Ana tem 1,5 m de altura, então é CORRETO afirmar que a altura do poste é de:
Alternativas:
- a) 1,0 m
- b) 2,3 m
- c) 5,9 m
- d) 2,6 m
- e) 2,0 m
Solução Passo a Passo:
A situação envolve proporcionalidade entre altura e sombra, já que Ana e o poste estão sob o mesmo sol.
Dados:
Altura de Ana: \( 1{,}5 \, \text{m} \)
Sombra de Ana: \( 2{,}4 \, \text{m} \)
Sombra do poste: \( 3{,}7 \, \text{m} \)
Sejam:
\[ h_{\text{Ana}} = 1{,}5,\quad s_{\text{Ana}} = 2{,}4,\quad s_{\text{Poste}} = 3{,}7,\quad h_{\text{Poste}} = x \]
Estabelecendo a proporção:
\[ \frac{1{,}5}{2{,}4} = \frac{x}{3{,}7} \]
Multiplicando cruzado:
\[ 1{,}5 \cdot 3{,}7 = 2{,}4 \cdot x \] \[ 5{,}55 = 2{,}4x \] \[ x = \frac{5{,}55}{2{,}4} = \boxed{2{,}3125 \approx 2{,}3 \, \text{m}} \]
Resposta correta: letra b.
📌 Aproveite também:
Questão 4
(EPCAR-MG) Observe a figura a seguir:
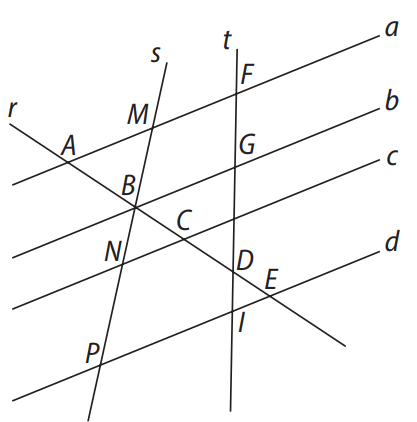
Nela, as retas a, b, c e d são paralelas e são interceptadas pelas retas transversais r, s e t.
Assim, as medidas dos segmentos, em cm, são:
- AB = y
- BC = 9
- CD = 10
- DE = 4
- FG = z
- GH = m
- HD = 5
- DI = 2
- MN = 16
- BN = 6
- BP = x
A soma AB + FH, em cm, é dada por um número divisível por:
- a) 3
- b) 4
- c) 7
- d) 11
Solução Passo a Passo:
Primeiro, determinamos o valor de \( AB \):
Sabendo que \( MB = 10 \) (pois \( MN = 16 \) e \( BN = 6 \)), e usando a proporcionalidade:
\[ \frac{AB}{MB} = \frac{BC}{BN} \] \[ \frac{AB}{10} = \frac{9}{6} \] \[ AB = 10 \cdot \frac{9}{6} = 15 \]
Agora, para calcular \( GH \), usamos os segmentos \( DE = 4 \), \( DI = 2 \), \( BC = 9 \), \( CD = 10 \), e \( HD = 5 \):
Sabendo que \( BD = 19 \) (pois \( BC = 9 \), \( CD = 10 \)), podemos usar a relação:
\[ \frac{DE}{DI} = \frac{BD}{GD} \] \[ \frac{4}{2} = \frac{19}{m + 5} \] \[ 2 = \frac{19}{m + 5} \] \[ 2(m + 5) = 19 \Rightarrow m = 4{,}5 \]
Agora usamos outra relação para determinar \( FG \):
\[ \frac{AB}{FG} = \frac{BC}{GH} \] \[ \frac{15}{FG} = \frac{9}{4{,}5} \Rightarrow \frac{15}{FG} = 2 \Rightarrow FG = \frac{15}{2} = 7{,}5 \]
Com \( FG = 7{,}5 \) e \( GH = 4{,}5 \), temos:
\[ FH = 7{,}5 + 4{,}5 = 12 \]
Por fim:
\[ AB + FH = 15 + 12 = \boxed{27} \]
Como \( 27 \div 3 = 9 \), temos um número divisível por 3.
Resposta correta: letra a.
📌 Aproveite também:
Questão 5
(UFU-MG) Uma área delimitada pelas Ruas 1 e 2 e pelas Avenidas A e B tem a forma de um trapézio \( ADD’A’ \), com \( AD = 90 \, \text{m} \) e \( A’D’ = 135 \, \text{m} \), como mostra o esquema da figura abaixo:
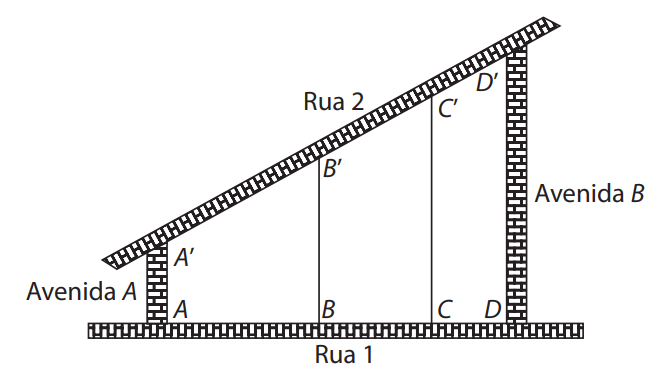
Essa área foi dividida em terrenos \( ABB’A’ \), \( BCC’B’ \) e \( CDD’C’ \), todos na forma trapezoidal, com bases paralelas às avenidas, tais que:
- \( AB = 40 \, \text{m} \)
- \( BC = 30 \, \text{m} \)
- \( CD = 20 \, \text{m} \)
De acordo com essas informações, a diferença, em metros, \( A’B’ – C’D’ \) é igual a:
- a) 20
- b) 30
- c) 15
- d) 45
Solução Passo a Passo:
O enunciado nos informa que os triângulos e trapézios são semelhantes, então podemos aplicar o Teorema de Tales para obter os valores de \( A’B’ \) e \( C’D’ \).
Sabemos que:
\[ \frac{AD}{A’D’} = \frac{AB}{A’B’} \Rightarrow \frac{90}{135} = \frac{40}{A’B’} \]
Multiplicando cruzado:
\[ 90 \cdot A’B’ = 135 \cdot 40 \] \[ A’B’ = \frac{135 \cdot 40}{90} = \frac{5400}{90} = 60 \]
Agora aplicamos o mesmo raciocínio para \( C’D’ \):
\[ \frac{AD}{A’D’} = \frac{CD}{C’D’} \Rightarrow \frac{90}{135} = \frac{20}{C’D’} \] \[ C’D’ = \frac{135 \cdot 20}{90} = \frac{2700}{90} = 30 \]
Portanto:
\[ A’B’ – C’D’ = 60 – 30 = \boxed{30 \, \text{m}} \]
Resposta correta: letra b.
📌 Aproveite também:
Questão 6
(UEA-AM) A circunferência \( \gamma \) está inscrita no triângulo isósceles \( ABC \) de altura \( 12 \, \text{cm} \) e base medindo \( 10 \, \text{cm} \), conforme a figura:
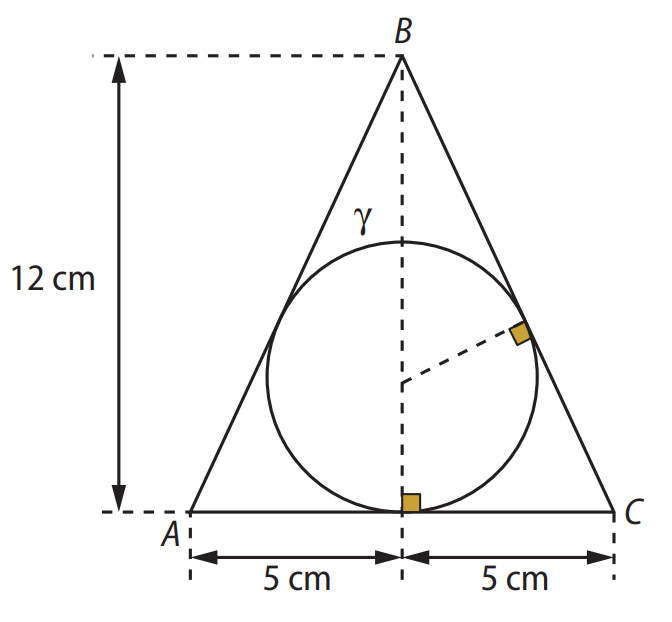
O raio da circunferência \( \gamma \) mede:
- a) \( \dfrac{16}{3} \) cm
- b) \( \dfrac{14}{5} \) cm
- c) \( \dfrac{18}{7} \) cm
- d) \( \dfrac{10}{3} \) cm
- e) \( \dfrac{12}{5} \) cm
Solução Passo a Passo:
Vamos usar o triângulo \( BPC \), que é retângulo, para aplicar o Teorema de Pitágoras e descobrir o valor de \( BC \):
\[ BC^2 = BP^2 + CP^2 \] \[ BC^2 = 12^2 + 5^2 = 144 + 25 = 169 \Rightarrow BC = \sqrt{169} = 13 \]
Agora, observamos os triângulos \( BOQ \) e \( BPC \), que são semelhantes (caso AA – dois ângulos iguais).
Usando a razão entre os lados correspondentes, temos:
\[ \frac{R}{5} = \frac{12 – R}{13} \]
Multiplicando cruzado:
\[ 13R = 5(12 – R) \Rightarrow 13R = 60 – 5R \Rightarrow 18R = 60 \Rightarrow R = \frac{60}{18} = \boxed{\frac{10}{3} \, \text{cm}} \]
Resposta correta: letra d.
📌 Aproveite também:
Questão 7
(Fuvest-SP) Na figura abaixo, as distâncias dos pontos \( A \) e \( B \) à reta \( r \) valem \( 2 \) e \( 4 \). As projeções ortogonais de \( A \) e \( B \) sobre essa reta são os pontos \( C \) e \( D \). Se a medida de \( \overline{CD} \) é \( 9 \), a que distância de \( C \) deverá estar o ponto \( E \), do segmento \( \overline{CD} \), para que \( \angle CEA \cong \angle DEB \)?
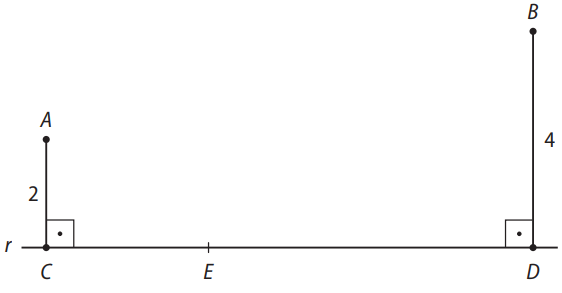
Alternativas:
- a) 3
- b) 4
- c) 5
- d) 6
- e) 7
Solução Passo a Passo:
Vamos usar semelhança de triângulos.
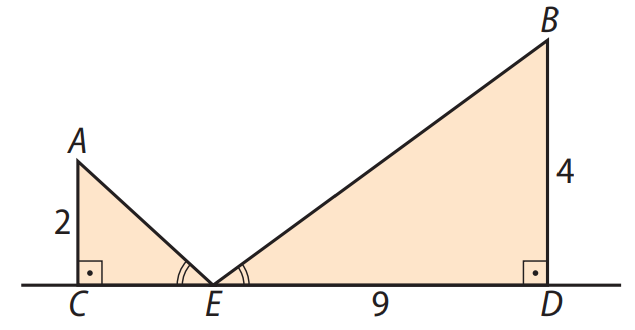
Queremos que os triângulos \( \triangle ACE \) e \( \triangle BDE \) sejam semelhantes, ou seja:
\[ \angle CEA \cong \angle DEB \quad \text{e} \quad \angle C \cong \angle D \ (\text{ambos retos}) \]
Então podemos escrever a proporção:
\[ \frac{ED}{CE} = \frac{4}{2} = 2 \]
Sabemos que \( CD = 9 \), então:
\[ ED = 9 – CE \Rightarrow \frac{9 – CE}{CE} = 2 \]
Multiplicando cruzado:
\[ 9 – CE = 2 \cdot CE \Rightarrow 9 = 3 \cdot CE \Rightarrow CE = \boxed{3} \]
Resposta correta: letra a.
📌 Aproveite também:
Questão 8
(IFPE) Ramon, Alexandre e Milton são alunos do curso de Informática no Campus Afogados da Ingazeira e estão testando um robô para participar de olimpíadas de robótica.
Um dos exercícios consistia em fazer o robô realizar os seguintes comandos:
- Andar 30 cm em linha reta;
- Realizar um giro de 90° à direita;
- Andar mais 40 cm em linha reta;
- Retornar ao ponto inicial no menor percurso possível.
Sobre o trajeto percorrido pelo robô, neste teste, é CORRETO afirmar que:
- a) forma um triângulo retângulo cuja hipotenusa mede 50 cm.
- b) forma um triângulo retângulo cujo perímetro mede 100 cm.
- c) forma um triângulo retângulo e isósceles.
- d) forma um paralelogramo cujo perímetro mede 140 cm.
- e) forma um paralelogramo cujas diagonais medem 50 cm.
Solução Passo a Passo:
O robô andou 30 cm em linha reta, virou 90° e andou mais 40 cm, formando dois lados de um triângulo.
Como o ângulo entre os segmentos é de 90°, o triângulo formado é retângulo.
Para retornar ao ponto inicial, o robô percorre a hipotenusa do triângulo.
Utilizando o Teorema de Pitágoras:
\[ x^2 = 30^2 + 40^2 \] \[ x^2 = 900 + 1600 = 2500 \] \[ x = \sqrt{2500} = \boxed{50 \, \text{cm}} \]
Resposta correta: letra a.
📌 Aproveite também:
Questão 9
(UFRGS-RS) Considere o retângulo \(ABCD\) de lados \( AB = 4 \) e \( AD = 2 \), e o ponto médio \( M \) de \( AB \).
Traçando a reta mediatriz do lado \( AB \), determina-se o segmento \( MN \), com \( N \) na interseção da mediatriz com \( DC \).
Considere um ponto \( P \) construído sobre o segmento \( MN \), e os segmentos \( PD \) e \( PC \), como mostra a figura abaixo.
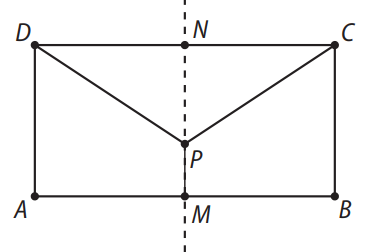
Tomando \( x \) como a medida do segmento \( PN \), considere \( S(x) \) a função que expressa a soma das medidas dos segmentos \( PM \), \( PD \) e \( PC \) em função de \( x \).
Para \( 0 \leq x \leq 2 \), \( S(x) \) é:
- a) \( x + 2\sqrt{x^2 + 4} \)
- b) \( (2 – x) + 2(x^2 + 4) \)
- c) \( (2 – x) + \sqrt{x^2 + 4} \)
- d) \( x + \sqrt{x^2 + 4} \)
- e) \( (2 – x) + 2\sqrt{x^2 + 4} \)
Solução Passo a Passo:
Sabemos que \( AD = 2 \), e como \( P \) está a \( x \) unidades de \( N \), a distância de \( P \) até \( M \) será:
\[ PM = 2 – x \]
Pelo desenho, temos também \( CP = PD \). Podemos calcular a medida de \( CP \) (ou \( PD \)) usando o Teorema de Pitágoras:
\[ CP^2 = x^2 + 2^2 = x^2 + 4 \Rightarrow CP = \sqrt{x^2 + 4} \]
Assim, a função que representa a soma dos três segmentos é:
\[ S(x) = PM + PD + PC \] \[ S(x) = (2 – x) + \sqrt{x^2 + 4} + \sqrt{x^2 + 4} \] \[ S(x) = (2 – x) + 2\sqrt{x^2 + 4} \]
Resposta correta: letra e.
📌 Aproveite também:
Questão 10
(Cefet-MG) Na figura a seguir, o segmento \( \overline{AC} \) representa uma parede cuja altura é \( 2{,}9 \, \text{m} \). A medida do segmento \( \overline{AB} \) é \( 1{,}3 \, \text{m} \), e o segmento \( \overline{CD} \) representa o beiral da casa.
Os raios de sol \( r_1 \) e \( r_2 \) passam ao mesmo tempo pela casa e pelo prédio, respectivamente. O prédio possui \( 8 \, \text{m} \) de altura e está a \( 3 \, \text{m} \) da parede da casa.
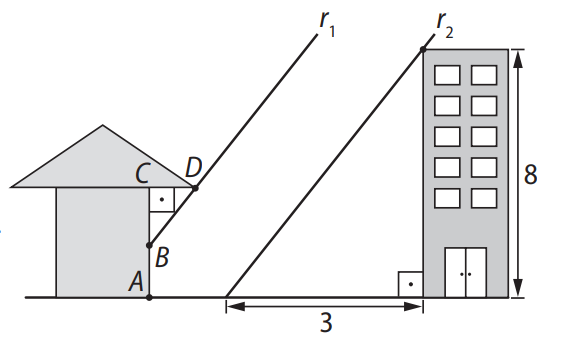
Sabendo que \( r_1 \parallel r_2 \), o comprimento do beiral \( \overline{CD} \), em metros, é:
- a) 0,60
- b) 0,65
- c) 0,70
- d) 0,75
Solução Passo a Passo:
A altura da parede é \( AC = 2{,}9 \, \text{m} \) e a parte abaixo do beiral mede \( AB = 1{,}3 \, \text{m} \). Assim, o segmento \( BC \), que representa a altura entre o beiral e a extremidade da sombra da parede, é:
\[ BC = AC – AB = 2{,}9 – 1{,}3 = 1{,}6 \, \text{m} \]
Sabemos que \( r_1 \parallel r_2 \), então, pelo Teorema de Tales, podemos escrever a seguinte proporção entre os segmentos semelhantes:
\[ \frac{8}{3} = \frac{BC}{CD} \Rightarrow \frac{8}{3} = \frac{1{,}6}{CD} \]
Multiplicando cruzado:
\[ 8 \cdot CD = 1{,}6 \cdot 3 \Rightarrow 8 \cdot CD = 4{,}8 \Rightarrow CD = \frac{4{,}8}{8} = \boxed{0{,}6 \, \text{m}} \]
Resposta correta: letra a.
📌 Aproveite também:
Questão 11
(FGV-SP) O paralelogramo \(ABCD\), indicado na figura abaixo, possui:
- \( BE = \dfrac{BC}{4} \)
- \( DF = \dfrac{AD}{3} \)
- \( G \) é o ponto de interseção de \( \overline{EF} \) com \( \overline{AC} \)
A área do triângulo \( GCE \) supera a do triângulo \( GAF \), aproximadamente:
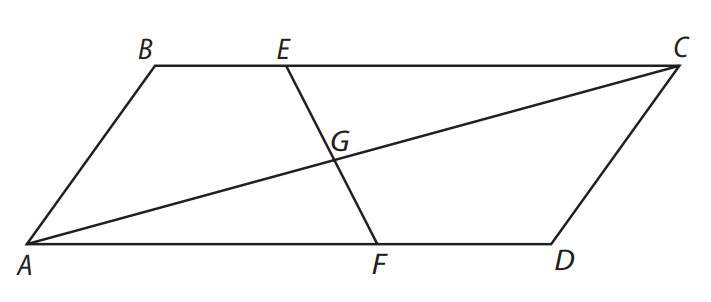
- a) 27%
- b) 25%
- c) 21%
- d) 11%
- e) 6%
Solução Passo a Passo:
Sabemos que:
\[ CE = \frac{3}{4} \cdot BC \quad \text{e} \quad AF = \frac{2}{3} \cdot AD \]
Como \( AD = BC \) (lados opostos de um paralelogramo), podemos reescrever:
\[ AF = \frac{2}{3} \cdot BC \]
Agora analisamos os triângulos \( GCE \) e \( GAF \). Ambos têm dois ângulos iguais (ângulo \( \widehat{A} \cong \widehat{C} \) e o ângulo comum \( \widehat{G} \)), então são semelhantes (caso AA).
A razão entre os lados correspondentes é:
\[ \frac{CE}{AF} = \frac{\frac{3}{4}BC}{\frac{2}{3}BC} = \frac{3}{4} \cdot \frac{3}{2} = \frac{9}{8} \]
A razão entre as áreas dos triângulos semelhantes é o quadrado da razão dos lados:
\[ \left(\frac{9}{8}\right)^2 = \frac{81}{64} \approx 1{,}265625 \]
Isso representa um acréscimo de:
\[ 1{,}265625 – 1 = 0{,}265625 \approx \boxed{27\%} \]
Resposta correta: letra a.
📌 Aproveite também:
📏 Estude Mais: Relações Métricas no Triângulo Retângulo
Aprofunde seu conhecimento com o artigo completo que explica passo a passo como aplicar as relações métricas no triângulo retângulo. Ideal para quem deseja dominar esse tema com teoria e exemplos visuais!
🔗 Acessar o artigo agora
























