1º Caso de Semelhança de Triângulos: AA (Ângulo, Ângulo)
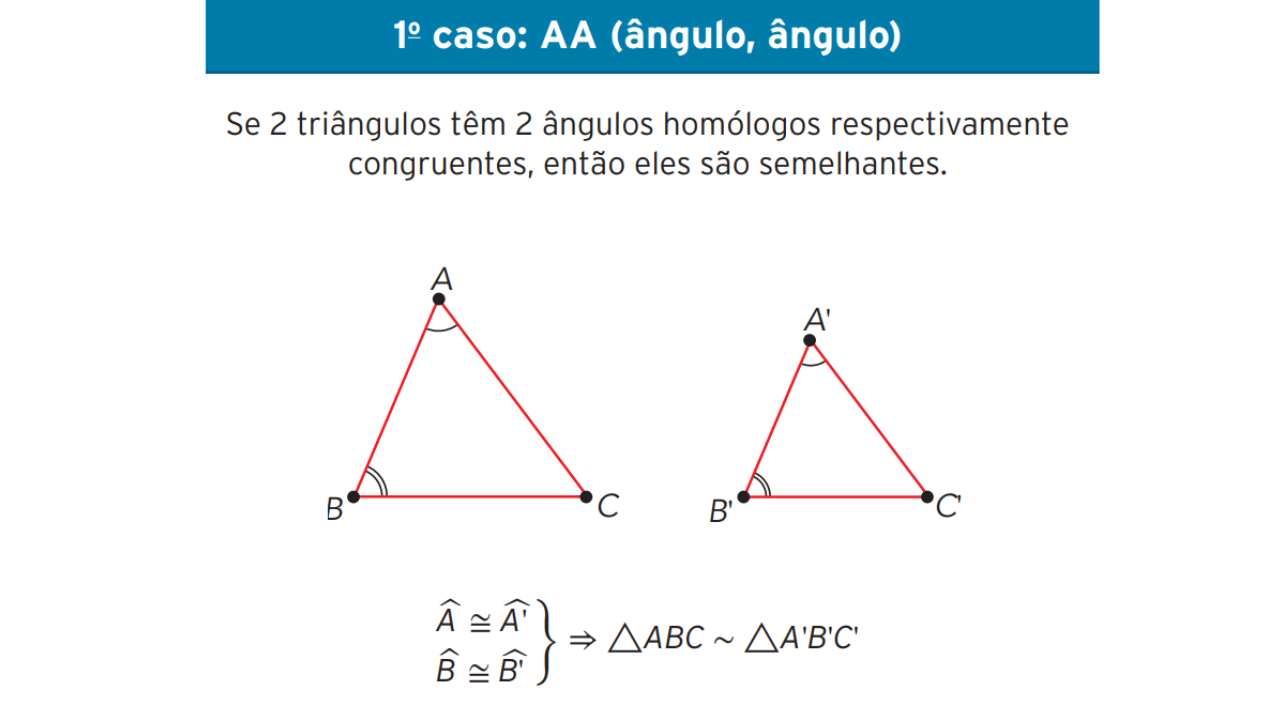
O primeiro caso de semelhança afirma que: se dois triângulos possuem dois ângulos homólogos congruentes, então eles são semelhantes.
Definição
Dois triângulos são semelhantes pelo caso Ângulo-Ângulo (AA) quando:
- Dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo.
- O terceiro ângulo também será congruente, já que a soma dos ângulos internos de qualquer triângulo é 180°.
Propriedades
- Ângulos correspondentes são iguais.
- Lados correspondentes estão em proporção.
- O Teorema de Tales é uma ferramenta importante para identificar triângulos semelhantes.
Exemplo Resolvido
Exemplo: No triângulo \(ABC\), temos os ângulos \( \hat{A}=40° \) e \( \hat{B}=60° \). Em outro triângulo \(A’B’C’\), temos \( \hat{A’}=40° \) e \( \hat{B’}=60° \). Esses triângulos são semelhantes?
Mostrar solução
Sim. Como dois ângulos correspondentes são iguais, pelo caso AA os triângulos são semelhantes.
📘 Bloco de Exercícios – Caso AA
Resolva os exercícios de múltipla escolha:
1) Se dois triângulos têm dois ângulos iguais de 50° e 60°, então podemos afirmar que:
- Não são semelhantes
- São semelhantes pelo caso AA
- São congruentes
- Não é possível concluir
Ver solução
Sim, pois dois ângulos iguais bastam para garantir a semelhança.
2) Dois triângulos possuem ângulos de medidas 40°, 80° e 60° no primeiro, e 40°, 60° e 80° no segundo. Eles são:
- Não semelhantes
- Semelhantes pelo caso AA
- Iguais
- Congruentes obrigatoriamente
Ver solução
Todos os ângulos correspondentes são iguais, logo são semelhantes (AA).
3) Um triângulo tem dois ângulos de 70° e 40°. Outro tem ângulos de 70° e 40°. Eles são semelhantes?
- Não
- Sim, pelo caso AA
- Apenas se os lados forem iguais
- Não se pode concluir
Ver solução
Sim, pois basta a igualdade de dois pares de ângulos.
4) Dois triângulos têm dois ângulos iguais, mas os lados são diferentes. Eles são:
- Congruentes
- Semelhantes
- Iguais
- Não semelhantes
Ver solução
Pelo caso AA, basta a igualdade de ângulos para a semelhança, mesmo com lados de comprimentos diferentes.
5) Em um triângulo, os ângulos medem 30°, 60° e 90°. Outro triângulo também possui ângulos 30°, 60° e 90°. Eles são:
- Não semelhantes
- Semelhantes pelo caso AA
- Congruentes
- Iguais
Ver solução
Sim, são semelhantes, pois possuem ângulos correspondentes iguais.
Links para aprofundar
📚 Produtos Recomendados
Para complementar seus estudos sobre semelhança de triângulos e geometria, confira os materiais disponíveis:
Esses materiais reúnem resumos visuais, exercícios resolvidos e listas de questões para concursos e vestibulares.






















