2º Caso de Semelhança de Triângulos: LLL (Lado, Lado, Lado)
O segundo caso de semelhança afirma que: se os três lados de um triângulo são proporcionais aos três lados de outro triângulo, então eles são semelhantes.
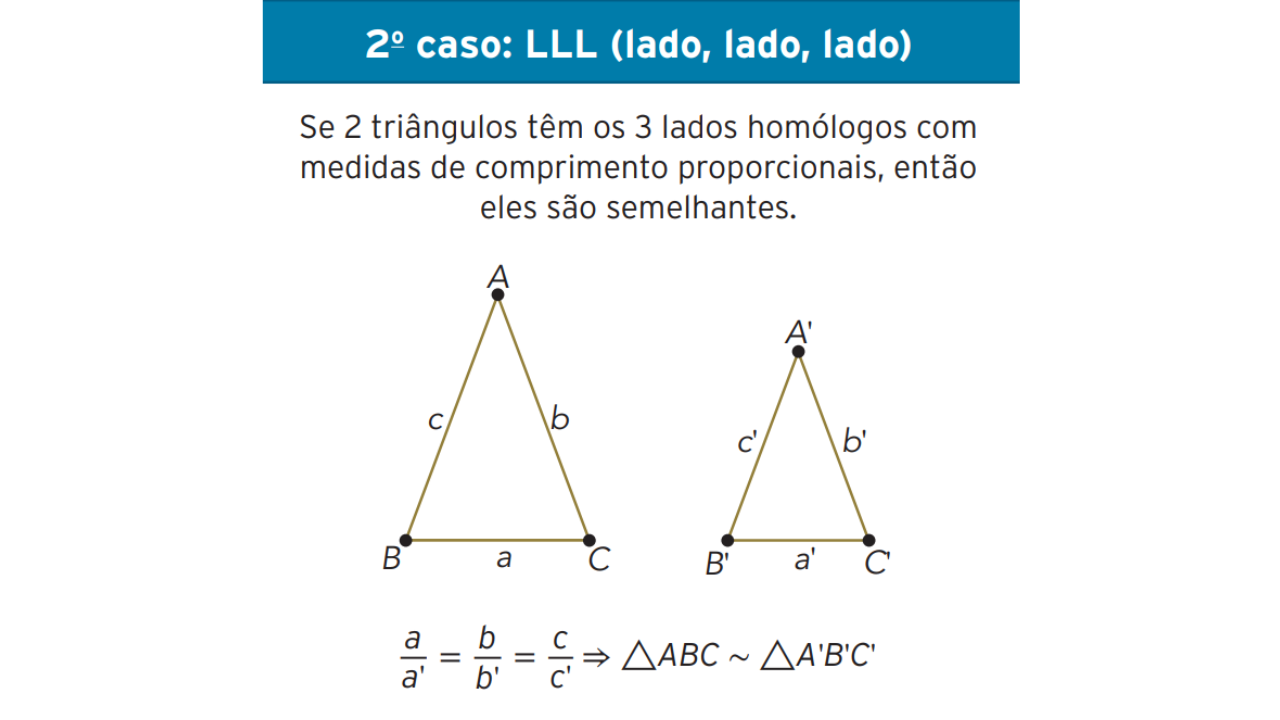
Definição
Dois triângulos são semelhantes pelo caso Lado-Lado-Lado (LLL) quando:
- As medidas dos três lados de um triângulo são proporcionais às medidas dos três lados correspondentes de outro triângulo.
Propriedades
- Lados correspondentes estão em proporção.
- Ângulos correspondentes são iguais (resultado da semelhança).
- As áreas dos triângulos semelhantes são proporcionais ao quadrado da razão de semelhança.
Exemplo Resolvido
Exemplo: Considere os triângulos \(ABC\) e \(A’B’C’\) com lados:
- \(ABC\): 3 cm, 4 cm e 5 cm
- \(A’B’C’\): 6 cm, 8 cm e 10 cm
Mostrar solução
As razões são: \( \frac{3}{6} = \frac{4}{8} = \frac{5}{10} = \frac{1}{2} \). Portanto, os triângulos são semelhantes pelo caso LLL.
📘 Bloco de Exercícios – Caso LLL
Resolva os exercícios de múltipla escolha:
1) Dois triângulos possuem lados 2, 4, 6 e 3, 6, 9. Eles são semelhantes?
- Não
- Sim, razão 2/3
- Sim, razão 1/3
- Somente se os ângulos também forem iguais
Ver solução
\(\frac{2}{3}=\frac{4}{6}=\frac{6}{9}=\frac{2}{3}\). Logo, semelhantes, razão \(2/3\).
2) Os lados de um triângulo medem 5, 7 e 9. Os lados de outro são 10, 14 e 18. Eles são:
- Congruentes
- Semelhantes (razão 1/2)
- Não semelhantes
- Isósceles
Ver solução
\(\frac{5}{10}=\frac{7}{14}=\frac{9}{18}=\frac{1}{2}\). Portanto, semelhantes, razão \(1/2\).
3) Os lados de dois triângulos são (3, 5, 7) e (6, 10, 14). Qual a razão de semelhança?
- 1/3
- 1/2
- 2
- 3
Ver solução
\(\frac{3}{6}=\frac{5}{10}=\frac{7}{14}=\frac{1}{2}\).
4) Dois triângulos são semelhantes pelo caso LLL. A razão de semelhança é 3. Se o lado de um mede 4 cm, o lado correspondente mede:
- 8 cm
- 12 cm
- 16 cm
- 20 cm
Ver solução
\(4 \cdot 3 = 12\).
5) Dois triângulos semelhantes pelo caso LLL têm áreas 25 cm² e \(A\). A razão de semelhança é 2. O valor de \(A\) é:
- 40 cm²
- 100 cm²
- 75 cm²
- 50 cm²
Ver solução
Áreas são proporcionais ao quadrado da razão: \(25 \cdot 2^2 = 25 \cdot 4 = 100\).
Links para aprofundar
📚 Produtos Recomendados
Aprimore seus estudos em geometria com nossos materiais exclusivos:
Esses produtos oferecem resumos esquemáticos, exercícios resolvidos e listas de provas para treinar com eficiência.






















