3º Caso de Semelhança de Triângulos: LAL (Lado, Ângulo, Lado)
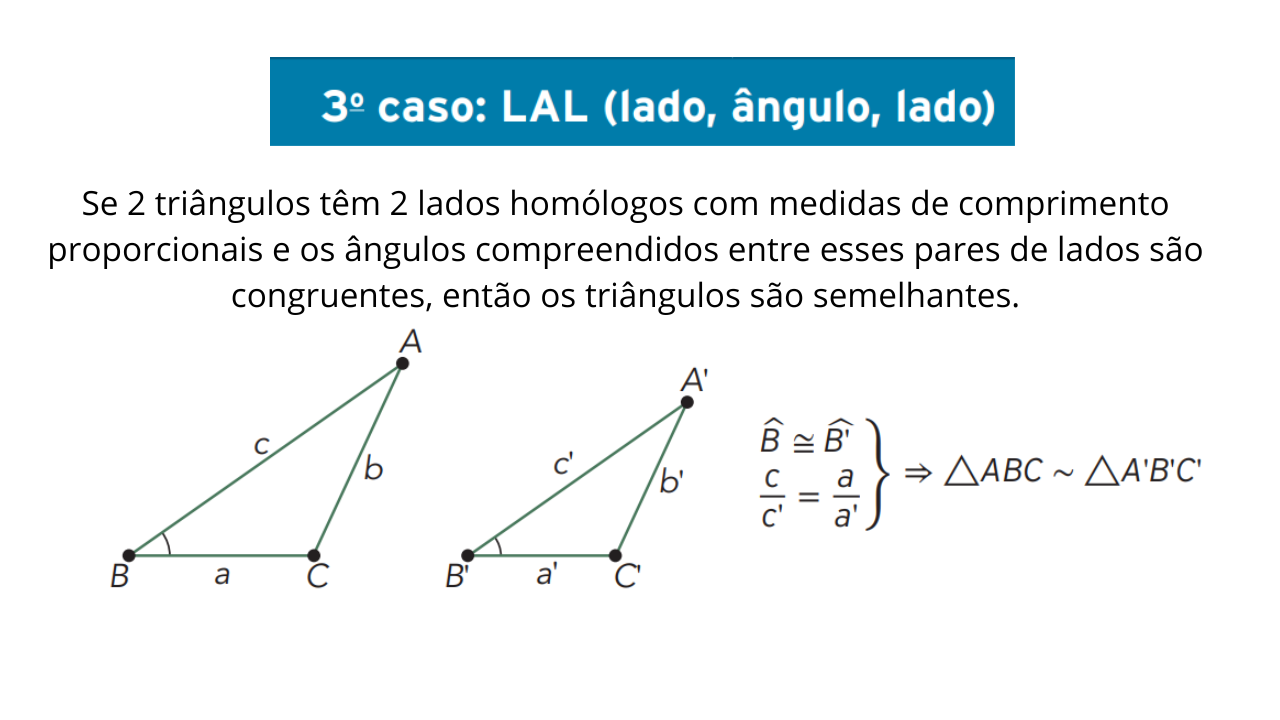
O terceiro caso de semelhança afirma que: se dois triângulos possuem dois lados proporcionais e o ângulo compreendido entre eles é congruente, então esses triângulos são semelhantes.
Definição
No caso Lado-Ângulo-Lado (LAL), dois triângulos são semelhantes quando:
- Dois pares de lados correspondentes estão em proporção;
- O ângulo compreendido entre esses lados é igual nos dois triângulos.
Propriedades
- Ângulos correspondentes são iguais.
- Lados correspondentes estão em proporção.
- A razão de semelhança é única e se aplica a todos os lados.
Exemplo Resolvido
Exemplo: Dois triângulos têm lados de medidas:
- \(ABC\): 4 cm, 6 cm e ângulo de 60° entre eles;
- \(A’B’C’\): 8 cm, 12 cm e ângulo de 60° entre eles.
Mostrar solução
As razões são \( \frac{4}{8} = \frac{6}{12} = \frac{1}{2} \). O ângulo é igual (60°). Logo, os triângulos são semelhantes pelo caso LAL, com razão de semelhança 1/2.
📘 Bloco de Exercícios – Caso LAL
Resolva os exercícios de múltipla escolha:
1) Dois triângulos têm lados 5 cm e 7 cm com ângulo de 90° entre eles; outro triângulo tem lados 10 cm e 14 cm com ângulo de 90°. Eles são semelhantes?
- Não
- Sim, razão 1/2
- Sim, razão 2
- Apenas se os outros ângulos forem iguais
Ver solução
\(\frac{5}{10}=\frac{7}{14}=1/2\). O ângulo é congruente (90°). Logo, semelhantes, razão 1/2.
2) Um triângulo tem lados 3 cm e 4 cm com ângulo de 60°. Outro triângulo tem lados 6 cm e 8 cm com ângulo de 60°. A razão de semelhança é:
- 1/4
- 2
- 1/2
- 3
Ver solução
\(\frac{3}{6}=\frac{4}{8}=1/2\). Razão de semelhança 1/2.
3) Dois triângulos têm lados proporcionais \(2/5\) e ângulos iguais entre eles. A razão de suas áreas será:
- 2/5
- 4/25
- 5/2
- 9/25
Ver solução
A razão das áreas é o quadrado da razão de semelhança: \((2/5)^2 = 4/25\).
Links para aprofundar
📚 Produtos Recomendados
Aprenda semelhança de triângulos de forma visual e prática com nossos materiais:
Materiais completos com resumos esquemáticos, listas de exercícios e simulados de provas.






















