Em uma aula de revisão, escrevi essa conta no quadro e pedi que resolvessem sem ajuda. Alguns alunos começaram a “chutar” valores rapidamente. Outros pararam, respiraram fundo e seguiram a regra. No fim, os resultados foram bem diferentes — e a razão foi simples: ordem das operações.
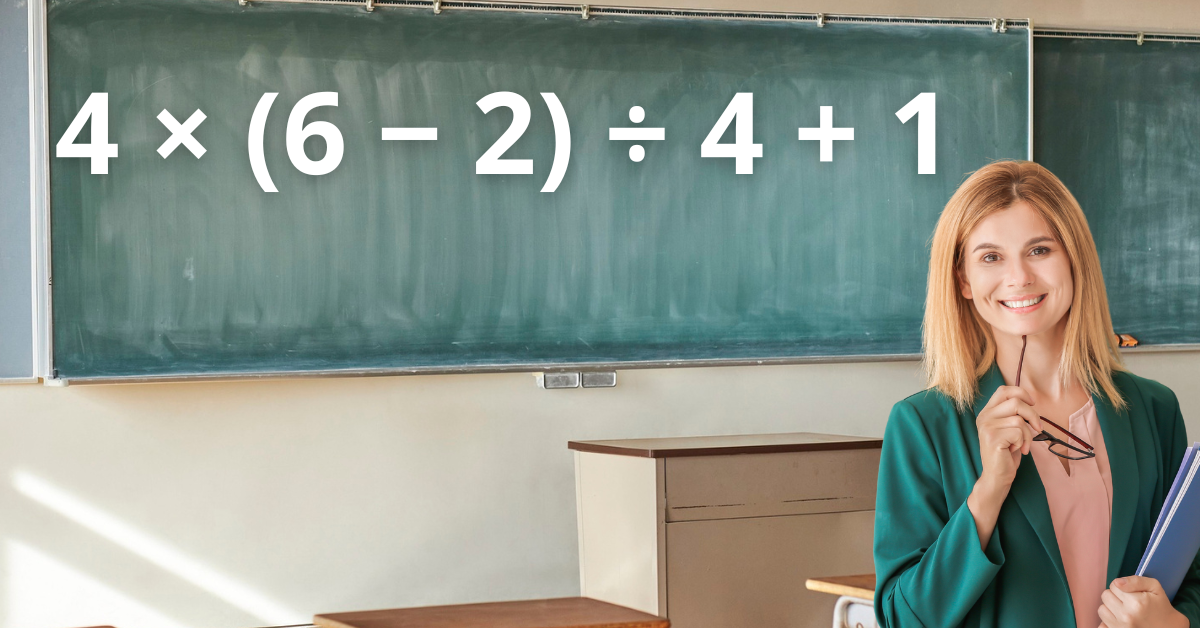
Essa expressão mistura parênteses, multiplicação, divisão e adição. É um exemplo clássico de expressão numérica que testa se a pessoa realmente conhece a ordem das operações.
Resolver “no chute” quase sempre leva ao erro.
Onde a maioria se engana
O erro mais comum é ignorar os parênteses ou resolver a divisão fora de ordem. Mas a regra é clara e não muda:
Resolução passo a passo
Expressão:
1) Resolva o que está dentro dos parênteses:
2) Substitua na expressão:
3) Faça multiplicação e divisão da esquerda para a direita:
4) Agora faça a adição:
Resposta final: 5
📌 Quer deixar de chutar e acertar sempre?
Treinar expressões completas ajuda a identificar rapidamente qual operação deve ser feita primeiro.
Conclusão
Na expressão 4 × (6 − 2) ÷ 4 + 1, resolver os parênteses primeiro faz toda a diferença. Seguindo a ordem correta das operações, o resultado final é 5.






















