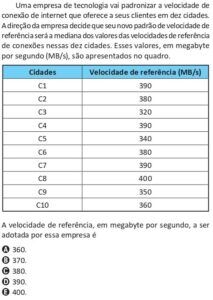
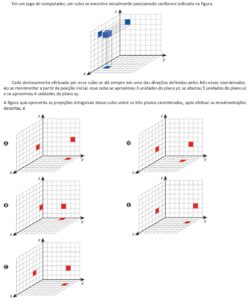
Explore uma seleção especial com 8 questões comentadas passo a passo sobre triângulos retângulos, teorema de Pitágoras, relações métricas, losangos e aplicações práticas com geometria. Cada exercício vem com enunciado ilustrado, solução interativa e links para mapas mentais e eBooks gratuitos. Ideal para quem está se preparando para provas, concursos ou quer dominar a geometria de forma visual e objetiva.
📘 Questão 1
(Enem/MEC) Na figura apresentada abaixo, que representa o projeto de uma escada com 5 degraus da mesma altura, o comprimento total do corrimão é igual a:
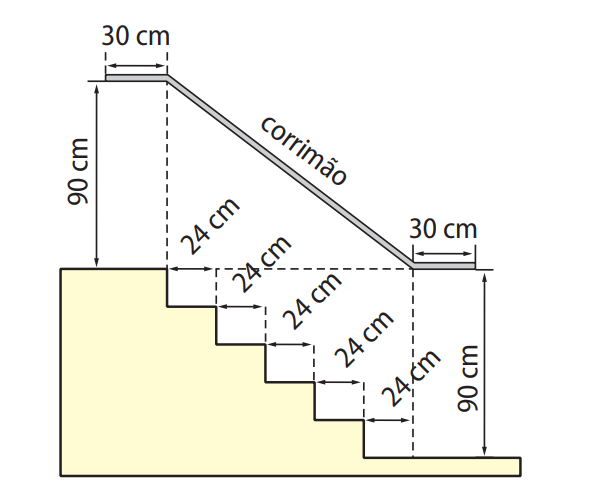
- a) 1,8 m
- b) 1,9 m
- c) 2,0 m
- d) 2,1 m
- e) 2,2 m
👀 Ver solução passo a passo
1. Clássico triângulo de Pitágoras:
Observamos que os catetos da escada formam proporção 3:4, o que indica o uso do triângulo pitagórico \( (3, 4, 5) \).
Somando os 5 degraus:
\[
24 + 24 + 24 + 24 + 24 = 120\,\text{cm}
\]
Altura total: \( 90\,\text{cm} \)
Aplicando o Teorema de Pitágoras: \[ 120^2 + 90^2 = C^2 \] \[ 14400 + 8100 = C^2 \] \[ C^2 = 22500 \Rightarrow C = \sqrt{22500} = 150\,\text{cm} \]
2. Abordagem alternativa (redução proporcional):
Podemos dividir os catetos por 30 para facilitar os cálculos:
\[
\frac{120}{30} = 4, \quad \frac{90}{30} = 3
\]
Aplicando o Teorema de Pitágoras:
\[
4^2 + 3^2 = C^2 \Rightarrow 16 + 9 = 25 \Rightarrow C = \sqrt{25} = 5
\]
Multiplicando novamente por 30 para voltar à proporção real:
\[
5 \times 30 = 150\,\text{cm}
\]
3. Corrimão completo:
Considerando as duas projeções horizontais de 30 cm em cada extremidade:
\[
150 + 30 + 30 = 210\,\text{cm} = 2{,}1\,\text{m}
\]
✅ Gabarito: Letra d) 2,1 m
🎯 Continue aprendendo com nossos materiais exclusivos:
📘 Questão 2
(UnB-DF) Em um triângulo retângulo, um dos catetos mede 16 metros. Determine, em metros, a medida da hipotenusa, sabendo que a medida desta excede a medida do outro cateto em oito metros.
👀 Ver solução passo a passo
1. Entendendo o problema:
Temos um triângulo retângulo com um cateto medindo \(16\ \text{m}\), e a hipotenusa é 8 metros maior que o outro cateto.
2. Definindo as variáveis:
Seja \(x\) o outro cateto.
Então, a hipotenusa será \(x + 8\).
3. Aplicando o Teorema de Pitágoras:
\[
x^2 + 16^2 = (x + 8)^2
\]
\[
x^2 + 256 = x^2 + 16x + 64
\]
4. Cancelando \(x^2\) dos dois lados:
\[
256 = 16x + 64
\Rightarrow 192 = 16x
\Rightarrow x = 12
\]
5. Calculando a hipotenusa:
\[
\text{Hipotenusa} = x + 8 = 12 + 8 = \boxed{20\ \text{m}}
\]
✅ Resposta correta: 20 metros
🎯 Continue aprendendo com nossos materiais exclusivos:
📘 Questão 3
Um triângulo retângulo tem sua hipotenusa medindo \(5\ \text{cm}\) e a altura relativa a essa hipotenusa com medida de \(2{,}4\ \text{cm}\). Com as informações fornecidas, é possível determinar as medidas, em centímetro, dos catetos? Justifique. Se não for possível, explicite pelo menos uma informação que tornaria possível resolver o problema.
👀 Ver solução passo a passo
1. Informações fornecidas:
– Hipotenusa \(c = 5\ \text{cm}\)
– Altura relativa à hipotenusa: \(h = 2{,}4\ \text{cm}\)
2. Aplicando a fórmula da área:
A área \(A\) de um triângulo pode ser calculada por:
\[
A = \frac{c \cdot h}{2} = \frac{5 \cdot 2{,}4}{2} = \frac{12}{2} = 6\ \text{cm}^2
\]
Portanto, conhecemos a área e a hipotenusa. Mas isso não é suficiente para determinar os catetos, pois eles podem variar mantendo a mesma área.
3. Relação métrica:
Sabemos que:
\[
h^2 = m \cdot n
\quad \text{e} \quad
m + n = c = 5
\]
Mas com apenas duas equações e três incógnitas (\(m, n, h\)), não é possível determinar unicamente os catetos \(a\) e \(b\), pois:
\[
a^2 = c \cdot m, \quad b^2 = c \cdot n
\]
sem saber o valor de \(m\) ou \(n\), não podemos achar \(a\) nem \(b\).
4. Conclusão:
Não é possível determinar os catetos apenas com a hipotenusa e a altura relativa a ela.
Seria necessário conhecer pelo menos:
- O valor de um dos catetos, ou
- Uma das projeções dos catetos sobre a hipotenusa.
✅ Resposta: Não, pois faltam dados.
🎯 Continue aprendendo com nossos materiais exclusivos:
📘 Questão 4
(FGV-SP) Na figura a seguir, \(ABCD\) é um retângulo e \(AMCN\) é um losango.
Determine a medida do segmento \(\overline{NB}\), sabendo que \(AB = 2AD = 20\,\text{cm}\).

👀 Ver solução passo a passo
1. Análise da figura:
Como \(AMCN\) é um losango, temos:
\[
AN = MC = AM = CN = x
\]
2. No triângulo \(ADN\):
\[
AD^2 + DN^2 = AN^2 \Rightarrow 10^2 + DN^2 = x^2 \Rightarrow 100 + DN^2 = x^2 \tag{1}
\]
3. No triângulo \(MBC\):
\[
MB = AB – AM = 20 – x
\]
\[
MB^2 + BC^2 = MC^2 \Rightarrow (20 – x)^2 + 10^2 = x^2
\]
Expandindo:
\[
(20 – x)^2 = 400 – 40x + x^2
\Rightarrow 400 – 40x + x^2 + 100 = x^2
\Rightarrow 500 – 40x = 0
\Rightarrow x = \frac{500}{40} = 12{,}5
\]
4. Com isso:
\[
AM = CN = 12{,}5\,\text{cm}
\quad\text{e}\quad
MB = 20 – 12{,}5 = 7{,}5\,\text{cm}
\]
5. Encontrando \(NB\):
No triângulo \(NBC\), temos:
\[
NB^2 = NC^2 + BC^2
\]
\[
\text{Como } NC = CD – DN \text{ e } DN = \sqrt{x^2 – AD^2}
\]
\[
DN = \sqrt{12{,}5^2 – 10^2} = \sqrt{156{,}25 – 100} = \sqrt{56{,}25} = 7{,}5\,\text{cm}
\Rightarrow NC = 20 – 7{,}5 = 12{,}5\,\text{cm}
\]\[
NB^2 = 12{,}5^2 + 10^2 = 156{,}25 + 100 = 256{,}25
\Rightarrow NB = \sqrt{256{,}25} \approx 16{,}007\,\text{cm}
\]
✅ Resposta final: Aproximadamente \( \boxed{16\ \text{cm}} \)
🎯 Continue aprendendo com nossos materiais exclusivos:
📄 Leia também:
Entenda de forma clara e prática as 🔺 Relações Métricas no Triângulo Retângulo com explicações passo a passo, figuras e aplicações diretas em exercícios. Ideal para quem está estudando trigonometria, geometria ou se preparando para concursos!
👉 Acessar o Artigo Completo📘 Questão 5
(UERJ) Segundo historiadores da matemática, a análise de padrões como os ilustrados a seguir possibilitou a descoberta das triplas pitagóricas.
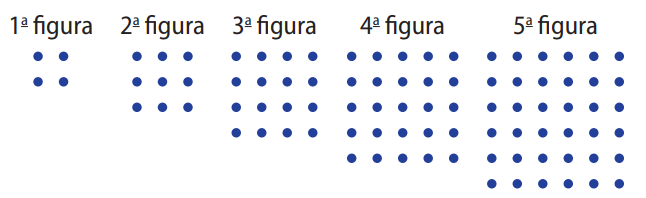
Observe que os números inteiros \(3^2\), \(4^2\) e \(5^2\), representados pelas 2ª, 3ª e 4ª figuras, satisfazem ao Teorema de Pitágoras. Dessa forma, \((3,\ 4,\ 5)\) é uma tripla pitagórica.
Os quadrados representados pelas 4ª, 11ª e \(n\)-ésima figuras determinam outra tripla pitagórica. Determine o valor de \(n\):
- a) 10
- b) 12
- c) 14
- d) 16
👀 Ver solução passo a passo
1. Análise do padrão:
Cada figura representa um quadrado de ordem crescente:
- 1ª figura → \(1^2 = 1\)
- 2ª figura → \(2^2 = 4\)
- 3ª figura → \(3^2 = 9\)
- 4ª figura → \(4^2 = 16\)
- …
A 11ª figura representa:
\[ 11^2 = 121 \]Desejamos encontrar o valor de \(n\) tal que as figuras 4ª, 11ª e \(n\) formem uma tripla pitagórica, ou seja:
\[ 4^2 + 11^2 = n^2 \]2. Aplicando o Teorema de Pitágoras:
\[ 16 + 121 = n^2 \] \[ 137 = n^2 \] \[ n = \sqrt{137} \approx 11{,}7 \]Como os quadrados são numerados com base em números inteiros, e não existe figura “11,7”, a figura mais próxima que representa esse valor é:
\[ n = 12 \]✅ Resposta correta: Letra b) 12
🎯 Continue aprendendo com nossos materiais exclusivos:
📘 Questão 6
(Unitau-SP) Uma rede de água potável ligará uma central de abastecimento, situada à margem de um rio de largura constante igual a 400 metros, a um conjunto habitacional localizado na margem oposta. A ligação será feita passando pelos pontos U, S e R, conforme ilustrado:
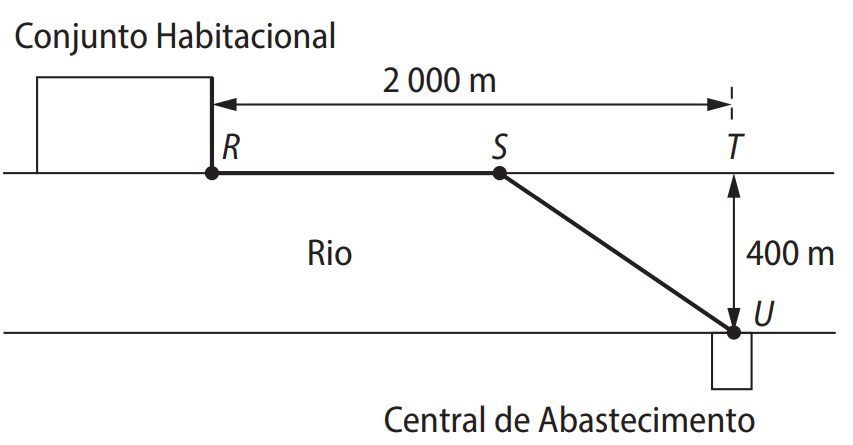
O custo por metro da tubulação é:
- R$ 830,00 por metro atravessando o rio
- R$ 400,00 por metro em terra
Sabendo que a distância entre o ponto \(R\) e o ponto \(S\) é de \(1.700\ \text{m}\), determine o custo total da instalação da tubulação.
- a) R\$ 1.611.000,00
- b) R\$ 1.012.000,00
- c) R\$ 1.132.000,00
- d) R\$ 1.095.000,00
- e) R\$ 1.321.000,00
👀 Ver solução passo a passo
1. Trecho em terra:
De \(R\) até \(S\), o encanamento é feito por terra.
2. Trecho no rio:
Do ponto \(S\) ao ponto \(U\), a instalação atravessa o rio. Precisamos calcular o comprimento do segmento \(SU\), que forma um triângulo retângulo com catetos:
Aplicando o Teorema de Pitágoras:
\[ SU^2 = ST^2 + TU^2 \] \[ SU^2 = 300^2 + 400^2 \] \[ SU^2 = 90.000 + 160.000 = 250.000 \] \[ SU = \sqrt{250.000} = 500\ \text{m} \]3. Cálculo do custo:
Trecho em terra:
\[ 1.700 \times 400 = R\$ 680.000 \]Trecho no rio:
\[ 500 \times 830 = R\$ 415.000 \]4. Custo total:
\[ C_{\text{total}} = 680.000 + 415.000 = \boxed{R\$ 1.095.000} \]✅ Resposta correta: Letra d) R\$ 1.095.000,00
🎯 Continue aprendendo com nossos materiais exclusivos:
📘 Questão 7
(Unichristus) Um drone, em um ponto \( A \), foi utilizado para localizar focos de incêndio na mata. Este drone está a uma altura \( H \) do solo e detecta dois focos nos pontos \( B \) e \( C \), como mostrado na figura:
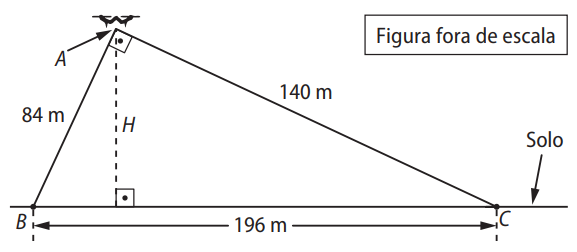
Sabendo que:
- \( AB = 84\ \text{m} \)
- \( AC = 140\ \text{m} \)
- \( BC = 196\ \text{m} \)
E que o triângulo \( ABC \) é retângulo em \( A \), determine a altura \( H \) do drone em relação ao solo.
- a) 45 m
- b) 50 m
- c) 55 m
- d) 60 m
- e) 65 m
👀 Ver solução passo a passo
O triângulo \( ABC \) é retângulo em \( A \), então aplicamos o Teorema de Pitágoras:
\( BC^2 = AB^2 + AC^2 \)
\[ 196^2 = 84^2 + 140^2 \] \[ 38416 = 7056 + 19600 \] \[ 38416 = 26656 \quad \text{(não confere!)} \]Na verdade, a hipotenusa deve ser o lado oposto ao ângulo reto. Como o ângulo reto é em \( A \), o lado oposto é \( BC = 196 \).
Para encontrar \( H \), usamos o triângulo retângulo \( ABC \), com catetos \( H \) e \( x \), e hipotenusa \( AC = 140 \).
\[ H^2 + x^2 = 140^2 \]Sabemos que:
\[ x = BC – AB = 196 – 84 = 112\ \text{m} \]\[ H^2 = 140^2 – 112^2 \] \[ H^2 = 19600 – 12544 = 7056 \] \[ H = \sqrt{7056} = \boxed{60\ \text{m}} \]✅ Resposta correta: Letra d) 60 m
🎓 Estude mais com nossos materiais gratuitos:
📄 Leia também:
Entenda de forma clara e prática as 🔺 Relações Métricas no Triângulo Retângulo com explicações passo a passo, figuras e aplicações diretas em exercícios. Ideal para quem está estudando trigonometria, geometria ou se preparando para concursos!
👉 Acessar o Artigo Completo