Questão 17 – OBMEP 2024
Cada um dos círculos desenhados no quadro deve ser pintado de azul, verde ou preto de modo que círculos ligados por um segmento tenham cores diferentes. De quantas maneiras podemos fazer essa pintura?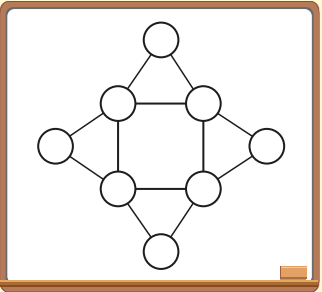
Alternativas:
- (A) 27
- (B) 8
- (C) 24
- (D) 18
- (E) 12
Ver Solução
Entendendo o enunciado:
A pintura deve ser feita com 3 cores (azul, verde, preto), garantindo que círculos ligados por segmentos não tenham a mesma cor.
Os círculos nos vértices (A, B, C, D) são estratégicos. Se definirmos A e B, o restante da figura fica determinado. Analisamos dois casos:
Caso 1: A e C têm a mesma cor.
– 3 escolhas para A
– 2 escolhas para B
– 2 escolhas para D (diferente de A)
Total: \(3 \times 2 \times 2 = 12\)
Caso 2: A e C têm cores diferentes.
– 3 escolhas para A
– 2 para B
– apenas 1 para D (a única cor diferente de A e C)
Total: \(3 \times 2 \times 1 = 6\)
Total de pinturas válidas:
\(12 + 6 = 18\) maneiras
Gabarito: Letra D
🧠 Mapas Mentais de Matemática





















