OBMEP 2024 – Nível 2 – Questão 10
Enunciado:
Pedro colocou os números 1, 2, 3, 4 e 5 nas casas do tabuleiro abaixo, um número em cada casa, sem repetir números nas linhas e nas colunas. Em seguida, ele somou os oito números colocados na primeira e na última coluna. Qual dos números abaixo não pode ser um resultado para a soma que Pedro fez?
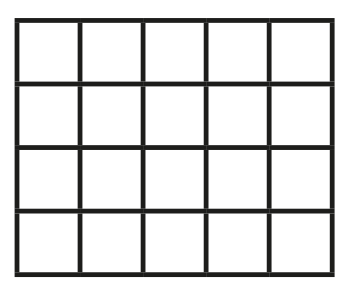
Alternativas:
- (A) 20
- (B) 23
- (C) 26
- (D) 25
- (E) 21
Ver Solução
Entendendo o enunciado: Devemos preencher uma tabela 5×5 com os números de 1 a 5 em cada linha e coluna, sem repetições. Depois, somar os números da primeira e da última coluna. A pergunta é: qual valor não pode aparecer como resultado dessa soma?
1. Considerando o menor valor possível:
Vamos tentar usar apenas os menores números (1, 2, 3, 4) nas colunas extremas, evitando o 5. Isso poderia levar à soma mínima.
Exemplo de arranjo válido:
1 _ _ _ 2
2 _ _ _ _
3 _ _ _ _
4 _ _ _ _
Soma: \(1 + 2 + 2 + 3 + 4 + 4 = 20\)
Porém, ao tentar preencher o restante do tabuleiro, percebemos que o número 5, que não foi usado nas colunas extremas, precisaria ser inserido 4 vezes nas outras colunas, o que não é possível sem repetir. Logo, a soma mínima não pode ser 20.
2. Considerando o maior valor possível:
Se colocarmos os maiores números (3, 4, 5) nas colunas extremas, conseguimos atingir somas maiores, como 27:
3 _ _ _ 4
4 _ _ _ _
5 _ _ _ _
1 _ _ _ _
2 _ _ _ _
3. Padrão geral das somas possíveis:
A tabela abaixo mostra as combinações possíveis para as colunas extremas:
| a | b | c | d | e | Soma |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 21 |
| 1 | 2 | 4 | 3 | 5 | 22 |
| 1 | 3 | 4 | 2 | 5 | 23 |
| 2 | 3 | 4 | 1 | 5 | 24 |
| 2 | 3 | 5 | 1 | 4 | 25 |
| 2 | 4 | 5 | 1 | 3 | 26 |
| 3 | 4 | 5 | 1 | 2 | 27 |
4. Conclusão:
Os valores possíveis para a soma das colunas extremas vão de 21 a 27.
Portanto, o valor 20 não pode ser obtido, e a resposta correta é:
Alternativa (A)
🧠 Mapas Mentais de Matemática





















