OBMEP 2024 – Nível 2 – Questão 11
Enunciado:
A figura é formada por quatro retângulos idênticos que se sobrepõem formando três quadrados. O lado maior de cada retângulo mede a cm e o lado menor mede b cm. Qual é a fórmula para o perímetro da figura, em centímetros?
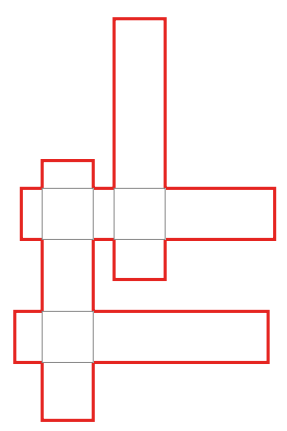
Alternativas:
- (A) 4(2a – b)
- (B) 4(a + b)
- (C) 4(a + 2b)
- (D) 4ab
- (E) 4(2a + b)
Ver Solução
Entendendo o enunciado: A figura formada tem 4 retângulos idênticos sobrepostos, criando 3 quadrados internos nas interseções. Precisamos calcular o perímetro da figura final.
1. Perímetro de cada retângulo:
O perímetro de um único retângulo seria: \( 2a + 2b \). Como temos 4 retângulos, o total inicial seria:
Perímetro total (sem sobreposição): \( 4(2a + 2b) = 8a + 8b \)
2. Ajuste pela sobreposição:
A sobreposição de dois retângulos cria um quadrado de lado \( b \), que está presente internamente, ou seja, esses lados não contam para o perímetro visível. Cada quadrado formado reduz o perímetro total em \( 4b \), pois retira dois lados de dois retângulos.
Como há 3 quadrados sobrepostos, a redução total será: \( 3 \times 4b = 12b \)
3. Resultado final:
Perímetro real = \( 8a + 8b – 12b = 8a – 4b = 4(2a – b) \)
Resposta correta: Alternativa (A)
Outra forma de visualizar:
Podemos deslocar os retângulos para obter uma figura equivalente sem sobreposição, como mostrado na imagem. O novo contorno tem largura \( a \) e altura \( 2a \), com partes de \( b \) subtraídas nas conexões. Isso confirma o mesmo resultado.






















