PROFMAT 2024 – Questão 13 | Soma em Progressão Aritmética
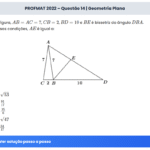
Seja \( \{a_1, a_2, \ldots, a_{100}\} \) uma progressão aritmética. Sabendo que:
\[ a_1 + a_2 + a_3 + \cdots + a_{99} + a_{100} = 2500 \]
É correto afirmar que \( a_2 + a_3 + \cdots + a_{98} + a_{99} \) é igual a:
(A) 2300
(B) 2350
(C) 2450
(D) 2451
(E) 2549
(B) 2350
(C) 2450
(D) 2451
(E) 2549
Resposta correta: (C) 2450.
A soma dos 100 termos de uma P.A. é: \[ S_{100} = \frac{a_1 + a_{100}}{2} \cdot 100 = 2500 \] Logo: \[ a_1 + a_{100} = 50 \]
Para encontrar a soma de \( a_2 + a_3 + \cdots + a_{99} \), basta subtrair o primeiro e o último termo da soma total: \[ S = 2500 – (a_1 + a_{100}) = 2500 – 50 = 2450 \]
🔗 Continue seus estudos com nossos recursos: