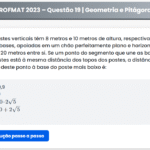
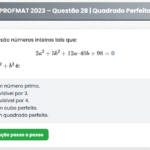
Duas locadoras de automóveis \( A \) e \( B \) cobram tarifas diferentes por um mesmo tipo de carro. A locadora \( A \) cobra 1 real por km rodado mais uma taxa fixa de 100 reais. A locadora \( B \) cobra 0,80 reais por km rodado mais uma taxa fixa de 200 reais.
Nessas condições, determine a distância mínima \( d \) tal que, se a distância percorrida for maior que \( d \), será mais vantajoso utilizar a locadora \( B \).
(B) 500 km
(C) 600 km
(D) 700 km
(E) 800 km
Resposta correta: (B) 500 km.
Indicando por \( A(x) \) e \( B(x) \) os valores cobrados pelas locadoras por \( x \) km rodados, temos: \[ A(x) = x + 100 \quad \text{e} \quad B(x) = 0,8x + 200 \]
Para que \( B \) seja mais vantajosa: \[ A(x) > B(x) \quad \Rightarrow \quad x + 100 > 0,8x + 200 \]
Resolvendo a inequação: \[ 0,2x > 100 \quad \Rightarrow \quad x > 500 \]
Portanto, a distância mínima \( d \) é de 500 km.
🔗 Continue seus estudos com nossos recursos: