Fórmula Área do Cilindro
O cilindro circular reto aparece em latas, copos, tubos e tanques. Aqui você encontra as fórmulas de área lateral (o “rótulo”) e área total (rótulo + tampas), uma demonstração por planificação, variações usuais, exemplos e exercícios com solução.
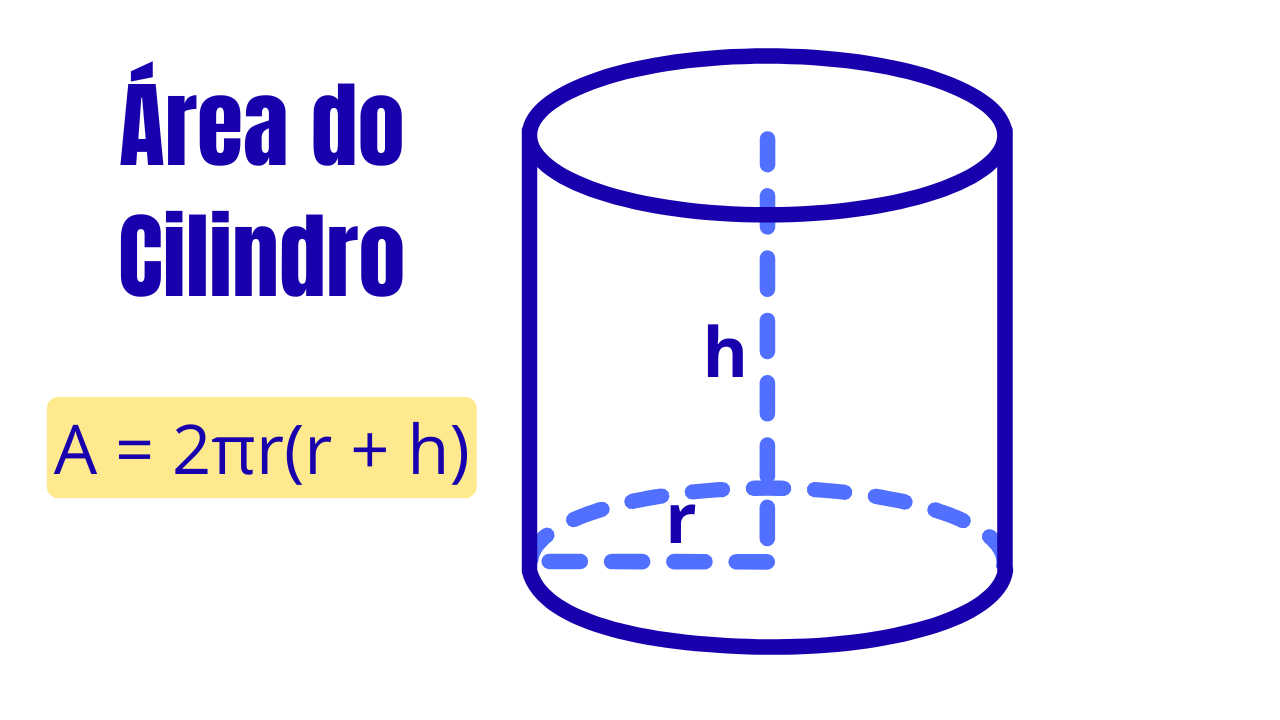
Notação usada: \(r\) = raio do círculo da base; \(h\) = altura (distância perpendicular entre os planos das bases). Unidades: se \(r\) e \(h\) estão em cm, a área sai em cm².
Quer ver o sólido completo? Consulte Cilindro e o texto irmão Fórmula Volume do Cilindro. Para panorama, veja Corpos redondos (compare com cone e esfera).
As fórmulas que você precisa
Área lateral (rótulo): \(\displaystyle A_L=2\pi r h\)
Área de uma base: \(\displaystyle A_{\text{base}}=\pi r^2\)
Área total (duas bases + lateral):
\(\displaystyle A_T=2\pi r h+2\pi r^2=2\pi r(r+h)\)
Se o problema disser “sem tampa” (aberto em cima): \(A=2\pi r h+\pi r^2\). Se disser “apenas o rótulo”: \(A=2\pi r h\).
De onde vem a fórmula? (planificação)
Ao planificar a superfície do cilindro, obtemos:
- Um retângulo (a superfície lateral) com largura igual à circunferência \(2\pi r\) e altura \(h\). Logo \(A_L=(2\pi r)\cdot h\).
- Dois círculos (as bases), cada um com área \(\pi r^2\), somando \(2\pi r^2\).
Somando tudo, \(A_T=A_L+2\pi r^2=2\pi r h+2\pi r^2=2\pi r(r+h)\).
Variações frequentes e observações
- Sem tampa (ou sem fundo): some apenas uma base: \(A=2\pi r h+\pi r^2\).
- Tubo oco (duas paredes visíveis): se as bordas planas das extremidades também forem expostas, a área é \(\displaystyle A=2\pi Rh+2\pi r h + 2\pi (R^2-r^2)\) (lateral externa + lateral interna + duas coroas). Se o enunciado ignorar as bordas (parede “fina”), use apenas \(2\pi Rh+2\pi r h\).
- Rótulo conhecido: se a “largura” do rótulo é \(2\pi r\), então \(r=\dfrac{\text{largura}}{2\pi}\) e \(A_L=\text{largura}\times h\).
- Diâmetro dado: se for dado o diâmetro \(d\), então \(r=d/2\).
Exemplos resolvidos
Exemplo 1 — Lata com tampa e fundo. \(r=4\) cm e \(h=10\) cm. Calcule a área total.
Ver solução
\(A_T=2\pi r(r+h)=2\pi\cdot4\cdot(4+10)=112\pi\approx \mathbf{351{,}86\ \text{cm}^2}\). (Lateral: \(80\pi\); duas bases: \(32\pi\)).
Exemplo 2 — Só o rótulo. Uma planificação tem retângulo de largura 25 cm (circunferência) e altura 20 cm. Encontre \(A_L\) e \(A_T\).
Ver solução
\(A_L=\text{largura}\times h=25\cdot20=\mathbf{500\ \text{cm}^2}\). \(r=\dfrac{25}{2\pi}\Rightarrow 2\pi r^2=25r\approx 25\cdot 3{,}979\approx 99{,}47\). \(A_T=500+99{,}47=\mathbf{599{,}47\ \text{cm}^2}\).
Exemplo 3 — Pote sem tampa. \(r=5\) cm, \(h=8\) cm. Calcule a área interior a revestir.
Ver solução
\(A=2\pi r h+\pi r^2=2\pi\cdot5\cdot8+25\pi=105\pi\approx \mathbf{329{,}87\ \text{cm}^2}\).
Exemplo 4 — Tubo oco (sem considerar bordas). \(R=6\) cm, \(r=5\) cm, \(h=10\) cm. Qual a área lateral visível?
Ver solução
\(A=2\pi Rh+2\pi r h=2\pi\cdot10\cdot(6+5)=220\pi\approx \mathbf{691{,}15\ \text{cm}^2}\). Se incluir as bordas: some \(2\pi(R^2-r^2)=22\pi\) ⇒ \(242\pi\approx 760{,}32\ \text{cm}^2\).
Exercícios (com solução)
Em todos: \(r\) = raio da base; \(h\) = altura. Use \(\pi\approx3{,}1416\).
1) Um cilindro reto possui \(r=3\) cm e \(h=12\) cm. Calcule \(A_L\) e \(A_T\) (em cm²).
Mostrar solução
\(A_L=2\pi rh=72\pi\approx 226{,}19\). \(A_T=2\pi r(r+h)=2\pi\cdot3\cdot15=90\pi\approx 282{,}74\).
2) Um pote sem tampa tem \(r=4\) cm e \(h=10\) cm. Qual a área a revestir por dentro?
Mostrar solução
\(A=2\pi rh+\pi r^2=80\pi+16\pi=96\pi\approx 301{,}59\ \text{cm}^2\).
3) O rótulo de uma lata mede 22 cm de largura (circunferência) por 12 cm de altura. Encontre a área total da lata (rótulo + duas tampas).
Mostrar solução
Rótulo: \(A_L=22\cdot12=264\). \(r=\frac{22}{2\pi}= \frac{11}{\pi}\approx 3{,}501\). \(2\pi r^2\approx 77{,}03\). \(A_T\approx 264+77{,}03=\mathbf{341{,}03\ \text{cm}^2}\).
4) Sabendo que \(A_T=112\pi\) cm² e \(r=4\) cm, determine \(h\).
Mostrar solução
\(112\pi=2\pi\cdot4(r+h)\Rightarrow 112=8(r+h)\Rightarrow r+h=14\Rightarrow h=\mathbf{10\ \text{cm}}\).
5) Um tanque será pintado por fora com tampa e sem fundo. Dados \(r=1{,}2\) m e \(h=2{,}5\) m, calcule a área a pintar (m²).
Mostrar solução
\(A=2\pi rh+\pi r^2=2\pi\cdot1{,}2\cdot2{,}5+\pi\cdot1{,}2^2=6\pi+1{,}44\pi=7{,}44\pi\approx \mathbf{23{,}36\ \text{m}^2}\).
6) Um tubo oco (parede fina) tem \(R=6\) cm, \(r=5\) cm e \(h=10\) cm. Qual a área lateral visível (sem considerar as bordas)?
Mostrar solução
\(A=2\pi Rh+2\pi r h=2\pi\cdot10(6+5)=220\pi\approx \mathbf{691{,}15\ \text{cm}^2}\).
7) Uma empresa vai plastificar apenas a lateral de um cilindro de \(r=6\) cm e \(h=12\) cm. Qual a área de filme necessária?
Mostrar solução
\(A_L=2\pi rh=2\pi\cdot6\cdot12=144\pi\approx \mathbf{452{,}39\ \text{cm}^2}\).
8) O fabricante quer dobrar \(A_T\) mantendo \(h\) fixo. Por qual fator o raio deve ser multiplicado?
Mostrar solução
\(A_T=2\pi r(r+h)\). Para \(h\) constante, dobrar \(A_T\) equivale a resolver \(k\,r(r+h)=2\,r(r+h)\Rightarrow k=\mathbf{2}\). (O raio deve dobrar.)





















